题目内容
17.甲、乙两艘客轮同时离开港口P,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B.若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,求乙客轮的航行方向.分析 依照题意画出图形,根据路程=速度×时间可求出PA、PB,根据PA、PB、AB的长度,利用勾股定理的逆运用即可得出∠APB=90°,结合∠NPA的度数即可求出∠SPB的度数,此题得解.
解答 解:依照题意画出图形,如图所示.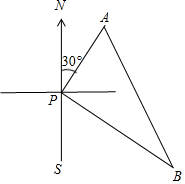
PA=40×15=600,PB=40×20=800,AB=1000,
∵6002+8002=10002,
∴PA2+PB2=AB2,
∴△APB为直角三角形,且∠APB=90°.
∵∠NPA=30°,
∴∠SPB=60°,
∴乙客轮的航行方向为南偏东60°.
点评 本题考查了勾股定理的应用以及方向角,根据PA、PB、AB的长度,利用勾股定理的逆运用找出∠APB=90°是解题的关键.

练习册系列答案
相关题目
8.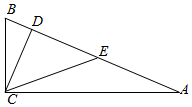 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )
 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )| A. | 2a | B. | 2$\sqrt{2}$a | C. | 3a | D. | $\frac{4\sqrt{3}}{3}a$ |
2. 如图,AB∥CD,∠A=70°,则∠1的度数是( )
如图,AB∥CD,∠A=70°,则∠1的度数是( )
 如图,AB∥CD,∠A=70°,则∠1的度数是( )
如图,AB∥CD,∠A=70°,则∠1的度数是( )| A. | 130° | B. | 110° | C. | 100° | D. | 70° |
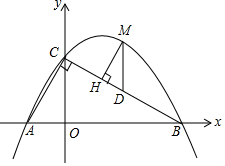 如图,直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+$\sqrt{3}$经过A,B两点.
如图,直线y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+$\sqrt{3}$经过A,B两点.