题目内容
16.如图,在坐标系中△ABO为直角三角形,且∠A=30°,点B(0,6).现有一动点P从点B出发向点A移动;另有一条平行于y轴的直线l从点A出发,沿着x轴向左运动.若点P与直线l同时出发,且运动速度均为每秒1个单位长度,运动时间为t(s),设直线l与线段AO交点为Q,与x轴交点为R,是否存在这样的时间t,使得△APQ为等腰三角形?若存在,求出这样的t值;若不存在,请说明理由.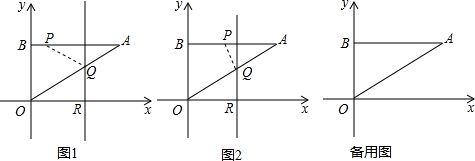
分析 存在这样的时间t,使得△APQ为等腰三角形,分三种情况考虑:若PQ=AQ,如图1所示;若AP=AQ,如图2所示;若AP=PQ,如图3所示,根据题意分别求出各自t的值即可.
解答 解:存在这样的时间t,使得△APQ为等腰三角形,
分三种情况考虑:
若PQ=AQ,如图1所示,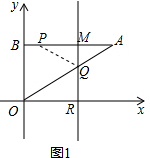
由题意得:BP=AM=t,
∵△APQ为等腰三角形,且QM⊥AP,
∴AM=PM=t,
∵Rt△AOB中,∠A=30°,BO=6,
∴OA=12,AB=6$\sqrt{3}$,
∴t+t+t=6$\sqrt{3}$,
解得:t=2$\sqrt{3}$s;
若AP=AQ,如图2所示,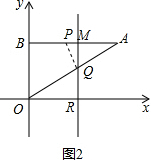
由题意得:BP=AM=t,AP=AB-BP=6$\sqrt{3}$-t,
在Rt△AMQ中,AQ=$\frac{AM}{cos30°}$=$\frac{t}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{3}}{3}$t,
∴6$\sqrt{3}$-t=$\frac{2\sqrt{3}}{3}$t,
解得:t=$\frac{6\sqrt{3}}{1+\frac{2\sqrt{3}}{3}}$=18(2-$\sqrt{3}$)=(36-18$\sqrt{3}$)s;
若AP=PQ,如图3所示,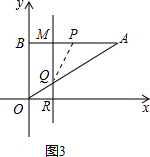
由题意得:BP=AM=t,AP=6$\sqrt{3}$-t,
在Rt△MQP中,MQ=$\frac{\sqrt{3}}{3}$t,∠MQP=30°,
∴PQ=$\frac{MQ}{cos30°}$=$\frac{\frac{\sqrt{3}}{3}t}{\frac{\sqrt{3}}{2}}$=$\frac{2}{3}$t,
∴6$\sqrt{3}$-t=$\frac{2}{3}$t,
解得:t=$\frac{18\sqrt{3}}{5}$s,
综上,存在这样的时间t,使得△APQ为等腰三角形,t的值为2$\sqrt{3}$s;(36-18$\sqrt{3}$)s;$\frac{18\sqrt{3}}{5}$s.
点评 此题属于一次函数综合题,涉及的知识有:等腰三角形的性质,锐角三角函数定义,勾股定理,以及三角函数性质,利用了分类讨论的思想,熟练掌握性质及定理是解本题的关键.

| A. | (x+2)2=3 | B. | (x+2)2=-5 | C. | (x+2)2=-3 | D. | (x+4)2=3 |
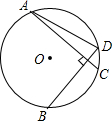 如图,⊙O的弦AC⊥BD,且$\widehat{AC}$=$\widehat{BD}$,若AD=2$\sqrt{2}$,求⊙O的半径.
如图,⊙O的弦AC⊥BD,且$\widehat{AC}$=$\widehat{BD}$,若AD=2$\sqrt{2}$,求⊙O的半径.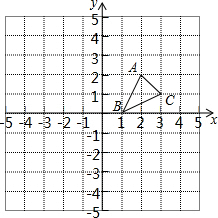 如图,平面直角坐标系中每个小方格均是边长为1个单位的正方形,△ABC的顶点均在格点上,点B的坐标为(1,0),按下列要求作图.
如图,平面直角坐标系中每个小方格均是边长为1个单位的正方形,△ABC的顶点均在格点上,点B的坐标为(1,0),按下列要求作图. .
.
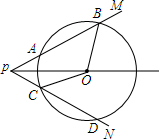 如图,点O是∠MPN的平分线上一点,以点O为圆心的圆和PM,PN分别相交于A,B,C,D四点,连接OB,OC.
如图,点O是∠MPN的平分线上一点,以点O为圆心的圆和PM,PN分别相交于A,B,C,D四点,连接OB,OC.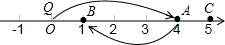 如图,数轴上一电子跳蚤Q从原点0出发,第1次沿数轴向右跳4个单位长度落在点A,第2次从点A出发沿数轴向左跳3个单位长度落在点B,第3次从点B沿数轴向右跳4个单位长度落在点C,第4次从点C出发沿数轴向左跳3个单位长度落在点D,…,按此规律继续跳动.
如图,数轴上一电子跳蚤Q从原点0出发,第1次沿数轴向右跳4个单位长度落在点A,第2次从点A出发沿数轴向左跳3个单位长度落在点B,第3次从点B沿数轴向右跳4个单位长度落在点C,第4次从点C出发沿数轴向左跳3个单位长度落在点D,…,按此规律继续跳动.