题目内容
2．若y=mx+m-1是关于x的正比例函数，求m的值．分析 由正比例函数的定义可得m-1=0，且m≠0，从而求解．
解答 解：根据题意，m-1=0，
解得：m=1．
点评 本题主要考查正比例函数的定义，解题关键是掌握正比例函数的定义条件：正比例函数y=kx的定义条件是：k为常数且k≠0，自变量次数为1．
练习册系列答案
相关题目
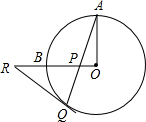如图，OA、OB是⊙O的两条互相垂直的半径，P为OB上任一点，AP的延长线交⊙O于点Q，过点Q作⊙O的切线交OB的延长线于点R，求证：RP=RQ．
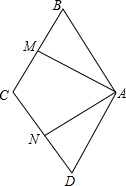已知：如图，在菱形ABCD中，∠BAD=120°，点M，N分别在BC和CD上，且∠MAN=60°．
如图，抛物线y=ax2+bx+c与y轴交于A点，过点A的直线y=$\frac{1}{2}$x+1与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C（3，0），又抛物线的对称轴为x=$\frac{17}{10}$．
12．用[x]表示不超过x的最大整数，把x-[x]称为x的小数部分．已知$t=\frac{1}{{2-\sqrt{3}}}$，a是t的小数部分，b是-t的小数部分，则$\frac{1}{2b}-\frac{1}{a}$=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | 1 | D． | $\sqrt{3}$ |