题目内容
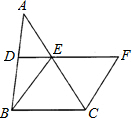 如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
如图,△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BCF=120°,求菱形BCFE的面积;
(3)若EC=9-m,BF=m-1(1<m<9),求菱形BCFE面积的最大值.
考点:菱形的判定与性质,二次函数的最值
专题:
分析:(1)从所给的条件可知,DE是△ABC中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=FE,所以四边形BCFE是菱形;
(2)∠BCF是120°,所以∠EBC为60°,所以菱形的边长也为6,求出菱形的高面积就可求;
(3)由菱形的面积=
EC•BF列出函数关系式,利用配方法求得二次函数最值即可.
(2)∠BCF是120°,所以∠EBC为60°,所以菱形的边长也为6,求出菱形的高面积就可求;
(3)由菱形的面积=
| 1 |
| 2 |
解答:(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC,且BC=2DE,
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形,
又∵BE=FE,
∴四边形BCFE是菱形;
(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为6,高为3
,
∴菱形的面积为6×3
=18
;
(3)解:设菱形BCFE面积为S,则
S=
EC•BF=
(9-m)(m-1)=-
(m-5)2+8.
∵该抛物线的开口方向向下,且1<m<9,
∴当m=5时,该抛物线的最大值是8.
答:菱形BCFE面积的最大值是8.
∴DE∥BC,且BC=2DE,
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形,
又∵BE=FE,
∴四边形BCFE是菱形;
(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为6,高为3
| 3 |
∴菱形的面积为6×3
| 3 |
| 3 |
(3)解:设菱形BCFE面积为S,则
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵该抛物线的开口方向向下,且1<m<9,
∴当m=5时,该抛物线的最大值是8.
答:菱形BCFE面积的最大值是8.
点评:本题考查菱形的判定和性质以及三角形中位线定理,以及菱形的面积的计算等知识点.

练习册系列答案
相关题目
一个盒子里有完全相同的三个小球,球上分别标有数字-2,1,4.随机摸出一个小球(不放回),其数字为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列多项式能用完全平方公式进行分解因式的是( )
| A、x2+1 |
| B、x2+2x+4 |
| C、x2-2x+1 |
| D、x2+x+1 |
 如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是
如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是 如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.
如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.