题目内容
甲乙两名同学做摸球游戏，他们把三个分别标有1，2，3的大小和形状完全相同的小球放在一个不透明的口袋中．
（1）求从袋中随机摸出一球，标号是1的概率；
（2）从袋中随机摸出一球后放回，摇匀后再随机摸出一球，若两次摸出的球的标号之和为偶数时，则甲胜；若两次摸出的球的标号之和为奇数时，则乙胜；试分析这个游戏是否公平？请说明理由．
（1）求从袋中随机摸出一球，标号是1的概率；
（2）从袋中随机摸出一球后放回，摇匀后再随机摸出一球，若两次摸出的球的标号之和为偶数时，则甲胜；若两次摸出的球的标号之和为奇数时，则乙胜；试分析这个游戏是否公平？请说明理由．
考点：游戏公平性,概率公式,列表法与树状图法
专题：探究型
分析：（1）由把三个分别标有1，2，3的大小和形状完全相同的小球放在一个不透明的口袋中，直接利用概率公式求解即可求得答案；
（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与甲胜，乙胜的情况，即可求得求概率，比较大小，即可知这个游戏是否公平．
（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与甲胜，乙胜的情况，即可求得求概率，比较大小，即可知这个游戏是否公平．
解答：解：（1）由于三个分别标有1，2，3的大小和形状完全相同的小球放在一个不透明的口袋中，
故从袋中随机摸出一球，标号是1的概率为：
；
（2）这个游戏不公平．
画树状图得：
∵共有9种等可能的结果，两次摸出的球的标号之和为偶数的有5种情况，两次摸出的球的标号之和为奇数的有4种情况，
∴P（甲胜）=
，P（乙胜）=
．
∴P（甲胜）≠P（乙胜），
故这个游戏不公平．
故从袋中随机摸出一球，标号是1的概率为：
| 1 |
| 3 |
（2）这个游戏不公平．
画树状图得：
∵共有9种等可能的结果，两次摸出的球的标号之和为偶数的有5种情况，两次摸出的球的标号之和为奇数的有4种情况，
∴P（甲胜）=
| 5 |
| 9 |
| 4 |
| 9 |
∴P（甲胜）≠P（乙胜），
故这个游戏不公平．
点评：本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．
练习册系列答案
相关题目
下列说法正确的个数是（ ）
①两个无理数的差一定是无理数；
②两个无理数的商一定是无理数；
③两个无理数的积可能是有理数；
④有理数和无理数的和一定是无理数；
⑤有理数和无理数的积一定是无理数．
①两个无理数的差一定是无理数；
②两个无理数的商一定是无理数；
③两个无理数的积可能是有理数；
④有理数和无理数的和一定是无理数；
⑤有理数和无理数的积一定是无理数．
| A、1个 | B、2个 | C、3个 | D、4个 |
下列多项式能用完全平方公式进行分解因式的是（ ）
| A、x2+1 |
| B、x2+2x+4 |
| C、x2-2x+1 |
| D、x2+x+1 |
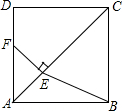如图，在正方形ABCD中，点E是对角线AC上一点，且CE=CD，过点E作EF⊥AC交AD于点F，连接BE．
如图，一条直线上有两只蚂蚁，甲蚂蚁在点A处，乙蚂蚁在点B处，假设两只蚂蚁同时出发，爬行方向只能沿直线AB在“向左”或“向右”中随机选择，并且甲蚂蚁爬行的速度比乙蚂蚁快．
