题目内容
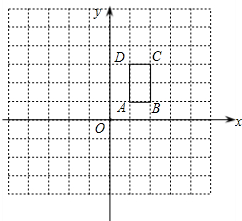 如图,矩形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).
如图,矩形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).(1)将矩形各顶点的横、纵坐标都乘以2,写出各对应点A1B1C1D1的坐标;顺次连接A1B1C1D1,画出相应的图形.
(2)求矩形A1B1C1D1与矩形ABCD的面积的比
(3)将矩形ABCD的各顶点的横、纵坐标都扩大n倍(n为正整数),得到矩形AnBnCnDn,则矩形AnBnCnDn与矩形ABCD的面积的比为
考点:作图-位似变换
专题:
分析:(1)根据题意得出对应点坐标进而画出图形;
(2)利用已知图形求出两图形面积,进而得出其面积比;
(3)利用横纵坐标变化得出相似比,进而得出矩形AnBnCnDn与矩形ABCD的面积的比.
(2)利用已知图形求出两图形面积,进而得出其面积比;
(3)利用横纵坐标变化得出相似比,进而得出矩形AnBnCnDn与矩形ABCD的面积的比.
解答: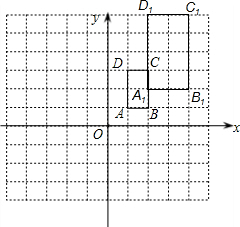 解:(1)如图所示:
解:(1)如图所示:
A1(2,2),B1(4,2),C1(4,6),D1(2,6);
(2)∵S矩形ABCD=1×2=2,S矩形A1B1C1D1=2×4=8,
∴矩形A1B1C1D1与矩形ABCD的面积的比:4:1;
(3)∵将矩形ABCD的各顶点的横、纵坐标都扩大n倍(n为正整数),得到矩形AnBnCnDn,
∴两图形相似比为:(n+1):1,
∴矩形AnBnCnDn与矩形ABCD的面积的比为:(n+1)2:1.
故答案为:(n+1)2:1.
 解:(1)如图所示:
解:(1)如图所示:A1(2,2),B1(4,2),C1(4,6),D1(2,6);
(2)∵S矩形ABCD=1×2=2,S矩形A1B1C1D1=2×4=8,
∴矩形A1B1C1D1与矩形ABCD的面积的比:4:1;
(3)∵将矩形ABCD的各顶点的横、纵坐标都扩大n倍(n为正整数),得到矩形AnBnCnDn,
∴两图形相似比为:(n+1):1,
∴矩形AnBnCnDn与矩形ABCD的面积的比为:(n+1)2:1.
故答案为:(n+1)2:1.
点评:此题主要考查了位似图形的性质,得出图形相似比是解题关键.

练习册系列答案
相关题目
下列多项式能用完全平方公式进行分解因式的是( )
| A、x2+1 |
| B、x2+2x+4 |
| C、x2-2x+1 |
| D、x2+x+1 |

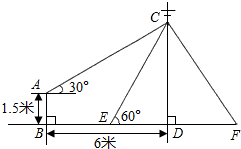 如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据:
如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据: