题目内容
8.解方程:(1)x2-4x=0
(2)x(x+1)=6
(3)x2-1=2(x+1)
(4)2x2-4x-5=0.
分析 (1)直接利用提取公因式法分解因式解方程得出答案;
(2)直接利用十字相乘法解方程得出答案;
(3)利用平方差公式再结合提取公因式法分解因式解方程得出答案;
(4)直接利用公式法解方程得出答案.
解答 解:(1)x2-4x=0
x(x-4)=0,
解得:x1=0,x2=4;
(2)x(x+1)=6
x2+x-6=0,
(x-2)(x+3)=0,
解得:x1=2,x2=-3;
(3)x2-1=2(x+1)
(x+1)(x-1)-2(x+1)=0,
(x+1)(x-1-2)=0,
解得:x1=-1,x2=3;
(4)2x2-4x-5=0.
b2-4ac=16+40=56>0,
则x=$\frac{4±\sqrt{56}}{4}$=$\frac{2±\sqrt{14}}{2}$
解得:x1=$\frac{2+\sqrt{14}}{2}$,x2=$\frac{2-\sqrt{14}}{2}$.
点评 此题主要考查了因式分解法解方程以及公式法/解方程,正确分解因式是解题关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
16. 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则有( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则有( )
 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则有( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则有( )| A. | a>0,b>0,c>0 | B. | a>0,b<0,c>0 | C. | a<0,b>0,c>0 | D. | a、b、c都小于0 |
 某校在一块一边筑墙(墙长15m)的空地上修建一矩形花园,如图,花园一边靠墙,另三边用总长为50m的栅栏围成,设BC边长为xm,花园面积为ym2.
某校在一块一边筑墙(墙长15m)的空地上修建一矩形花园,如图,花园一边靠墙,另三边用总长为50m的栅栏围成,设BC边长为xm,花园面积为ym2.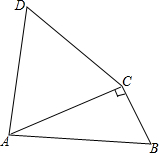 如图,△ABC中,∠ACB=90°,以AC为边作等边△ADC.
如图,△ABC中,∠ACB=90°,以AC为边作等边△ADC.