题目内容
17．在一个不透明的口袋里装有四个球，这四个球上分别标记数字-3、-1、0、2，除数字不同外，这四个球没有任何区别．（1）从中任取一球，求该球上标记的数字为负数的概率；
（2）从中任取一个球，球上标记的数字记为x，不放回再取一个球，球上标记的数字记为y，请你用树状图
或列表的方法，求点（x，y）位于坐标轴上的概率．
分析 （1）直接利用概率公式计算；
（2）画树状图展示所有12种等可能的结果数，再根据坐标轴上点的坐标特征，找出点（x，y）位于坐标轴上的结果数．然后根据概率公式求解．
解答 解：（1）从中任取一球，该球上标记的数字为负数的概率=$\frac{2}{4}$=$\frac{1}{2}$；
（2）画树状图为：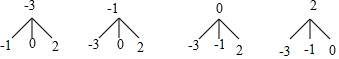
共有12种等可能的结果数，其中点（x，y）位于坐标轴上的结果数为6，
所以点（x，y）位于坐标轴上的概率=$\frac{6}{12}$=$\frac{1}{2}$．
点评 本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．
练习册系列答案
活力课时同步练习册系列答案
相关题目
5．小明所在的初三（1）班选举班长，两名候选人是李璐和王润．为了合理公正地搞好这次选举，决定进行一次演讲答辩与民主测评．邀请五位老师作为评委，对“演讲答辩”情况进行评价，全班50位同学参与民主测评．经过两位候选人各十分钟演讲答辩后，进行民主测评．结果如下表所示：
老师评定的演讲答辩得分表（ 单位：分）
民主测评票数统计表（ 单位：张）
班委会给出如下的得分计算方法：演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定；
民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分；
综合得分=演讲答辩得分×（1-a）+民主测评得分×a（0.5≤a≤0.8）．（设定a=0.6）
（1）请按以上计算方法，计算算出李璐和王润的综合得分；
（2）小明发现，只要改变字母a的值，两位候选人的综合得分就将改变，求当字母a的值在什么范围取值时，王润同学的得分会超过李璐同学．
老师评定的演讲答辩得分表（ 单位：分）
| 老师1 | 老师2 | 老师3 | 老师4 | 老师5 | |
| 李璐 | 90 | 92 | 94 | 95 | 88 |
| 王润 | 89 | 86 | 87 | 94 | 91 |
| “好”票数 | “较好”票数 | “一般”票数 | |
| 李璐 | 40 | 7 | 3 |
| 王润 | 42 | 4 | 4 |
民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分；
综合得分=演讲答辩得分×（1-a）+民主测评得分×a（0.5≤a≤0.8）．（设定a=0.6）
（1）请按以上计算方法，计算算出李璐和王润的综合得分；
（2）小明发现，只要改变字母a的值，两位候选人的综合得分就将改变，求当字母a的值在什么范围取值时，王润同学的得分会超过李璐同学．
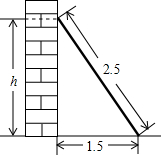如图，长2.5m的梯子靠在墙上，梯子的底部离墙的底端1.5m．
如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．△AOB绕点O逆时针旋转90°后得到△A1OB1．