题目内容
 如图所示,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,求∠APD的度数.
如图所示,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,求∠APD的度数.考点:旋转的性质,勾股定理的逆定理,正方形的性质
专题:
分析:如图,作旋转变换,将分散的条件PA、PD、PC集中到△PQC、△DQC中;证明PC2=PQ2+CQ2,根据勾股定理的逆定理求出∠PQC=90°;然后求出∠PQD=45°,得到∠DQC的度数,即可解决问题.
解答: 解:如图,将三角形APD绕点D沿逆时针旋转90°到达△CDQ的位置;
解:如图,将三角形APD绕点D沿逆时针旋转90°到达△CDQ的位置;
则∠PDQ=90°,QD=PD=2,QC=AP=1;由勾股定理得:
PQ2=22+22=8;而CQ2=1,PC2=32=9,
∴PC2=PQ2+CQ2,∠PQC=90°,
∵∠PQD=45°,
∴∠CQD=135°,
∴∠APD=∠CQD=135°.
 解:如图,将三角形APD绕点D沿逆时针旋转90°到达△CDQ的位置;
解:如图,将三角形APD绕点D沿逆时针旋转90°到达△CDQ的位置;则∠PDQ=90°,QD=PD=2,QC=AP=1;由勾股定理得:
PQ2=22+22=8;而CQ2=1,PC2=32=9,
∴PC2=PQ2+CQ2,∠PQC=90°,
∵∠PQD=45°,
∴∠CQD=135°,
∴∠APD=∠CQD=135°.
点评:该题主要考查了旋转变换的性质、勾股定理的逆定理等知识点的应用问题;解题的关键是作旋转变换,将分散的条件集中.

练习册系列答案
相关题目
张老师和李老师同时从学校出发,骑车去距学校20千米的县城购买书籍,张老师的汽车速度是李老师的1.5倍,结果张老师比李老师早到40分钟.设张老师骑车速度为x千米/小时,依题意,得到的方程是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向B以每秒2的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以每秒4的速度移动(不与点C重合),如果P,Q分别从A,B同时出发ts后,四边形APQC的面积为S.
如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向B以每秒2的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以每秒4的速度移动(不与点C重合),如果P,Q分别从A,B同时出发ts后,四边形APQC的面积为S. 如图,四边形ABCD是菱形,且∠A=60°,又E,F,G,H分别是菱形各边的中点,联结EH,FG,请判断六边形EBFGDH是一个怎样的图形?并说明你的结论.
如图,四边形ABCD是菱形,且∠A=60°,又E,F,G,H分别是菱形各边的中点,联结EH,FG,请判断六边形EBFGDH是一个怎样的图形?并说明你的结论.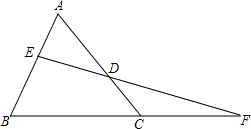 如图,在△ABC(AC>AB)的边AB、AC上分别取点E、D,使BE=CD,连接ED并延长交BC的延长线于点F,判断AB:AC=FD:EF是否成立.
如图,在△ABC(AC>AB)的边AB、AC上分别取点E、D,使BE=CD,连接ED并延长交BC的延长线于点F,判断AB:AC=FD:EF是否成立.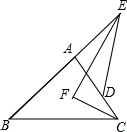 如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC=
如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC= 如图,两双曲线y=
如图,两双曲线y=