题目内容
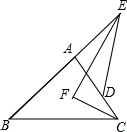 如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC=
如图,△ABC与△ADE有一个公共顶点A,且B,A,E共线,D在边AC上,∠E与∠C的平分线交于点F,若∠B=40°,∠EDA=56°,则∠EFC=考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据角平分线定义得出∠AED=2∠1,∠ACB=2∠2,根据三角形内角和定理和三角形的外角性质得出∠EAD=∠B+∠ACB=40°+2∠2,∠AED+∠ADE+∠EAD=180°,求出∠1+∠2=32°,根据三角形内角和定理和三角形的外角性质得出∠1+∠EDA+∠EMD=180°,∠EMD=∠EFC+∠2,推出∠1+∠EFC+∠2+56°=180°,即可得出答案.
解答:解:
∵EF平分∠BED,CF平分∠ACB,
∴∠AED=2∠1,∠ACB=2∠2,
∵在△EAD中,∠EAD=∠B+∠ACB=40°+2∠2,∠AED+∠ADE+∠EAD=180°,
∴40°+2∠2+2∠1+56°=180°,
∴∠1+∠2=32°,
∵在△EMD中,∠1+∠EDA+∠EMD=180°,∠EMD=∠EFC+∠2,
∴∠1+∠EFC+∠2+56°=180°,
∴∠EFC=92°,
故答案为:92°.

∵EF平分∠BED,CF平分∠ACB,
∴∠AED=2∠1,∠ACB=2∠2,
∵在△EAD中,∠EAD=∠B+∠ACB=40°+2∠2,∠AED+∠ADE+∠EAD=180°,
∴40°+2∠2+2∠1+56°=180°,
∴∠1+∠2=32°,
∵在△EMD中,∠1+∠EDA+∠EMD=180°,∠EMD=∠EFC+∠2,
∴∠1+∠EFC+∠2+56°=180°,
∴∠EFC=92°,
故答案为:92°.
点评:本题考查了三角形的外角性质,三角形的内角和定理的应用,能灵活运用定理进行推理和计算是解此题的关键,注意:①三角形的内角和定理等于180°,②三角形的一个外角等于和它不相邻的两个内角的和,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图.D是AB的中点,DE∥BC,AF⊥BC,垂足为F,AF交DE于G,则AG:AF的值为( )
如图.D是AB的中点,DE∥BC,AF⊥BC,垂足为F,AF交DE于G,则AG:AF的值为( )| A、1:2 | B、1:4 |
| C、2:1 | D、4:1 |
 如图,A、B对应的数为-1,-
如图,A、B对应的数为-1,- 如图所示,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,求∠APD的度数.
如图所示,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,求∠APD的度数. 如图,将一副三角尺如图所示叠放在一起,则
如图,将一副三角尺如图所示叠放在一起,则 已知等腰△ABC中,AB=AC=13,BC=10,求顶角∠A的正弦值.
已知等腰△ABC中,AB=AC=13,BC=10,求顶角∠A的正弦值. 如图,矩形ABCD的对角线相交于点O,BE⊥AC于点E,EB的延长线与∠ADC的角平线相交于点F,DF交AC于点M,求证:AC=BF.
如图,矩形ABCD的对角线相交于点O,BE⊥AC于点E,EB的延长线与∠ADC的角平线相交于点F,DF交AC于点M,求证:AC=BF. 如图所示,在△ABC中,∠ACB=90°,∠ADC=∠ACD,∠BCE=∠BEC,求∠DCE的度数.
如图所示,在△ABC中,∠ACB=90°,∠ADC=∠ACD,∠BCE=∠BEC,求∠DCE的度数. 如图,落地镜CD直立在地面上,小明在A处看到地面上的物体P的俯角为30°,看到该物体在落地镜CD中像Q的俯角为15°,小明眼睛的高度为1.6m,A,P,C在同一水平面上,若物体高度不计,问物体P离小明有多远?离落地镜有多远?(tan15°=2-
如图,落地镜CD直立在地面上,小明在A处看到地面上的物体P的俯角为30°,看到该物体在落地镜CD中像Q的俯角为15°,小明眼睛的高度为1.6m,A,P,C在同一水平面上,若物体高度不计,问物体P离小明有多远?离落地镜有多远?(tan15°=2-