题目内容
 如图,两双曲线y=
如图,两双曲线y=| k |
| x |
| 3 |
| x |
| 3 |
| x |
| k |
| x |
| k |
| x |
| 4 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:反比例函数的性质,反比例函数系数k的几何意义,反比例函数图象上点的坐标特征
专题:
分析:根据函数图象所在象限可得k>0,根据反比例函数的性质可得①正确;再根据函数解析式结合点B的横坐标为3,可得纵坐标,然后再根据4BD=3CD可得C点坐标;再利用C点坐标,根据图象上的点(x,y)的横纵坐标的积是定值k,即xy=k可得k的值;首先表示出B,C点坐标,进而得出BC的长,即可得出△ABC的面积.
解答:解:①∵双曲线y=
在第一象限,
∴k>0,
∴在每个象限内,y随x的增大而减小,故①正确;
②∵点B的横坐标为3,
∴y=-
=-1,
∴BD=1,
∵4BD=3CD,
∴CD=
,
∴点C的坐标为(3,
),故②错误;
③∵点C的坐标为(3,
),
∴k=3×
=4,故③正确;
④设B点横坐标为:x,则其纵坐标为:-
,故C点纵坐标为:
,
则BC=
+
=
,
则△ABC的面积为:
×x×
=3.5,故此选项错误.
故选:B.
| k |
| x |
∴k>0,
∴在每个象限内,y随x的增大而减小,故①正确;
②∵点B的横坐标为3,
∴y=-
| 3 |
| 3 |
∴BD=1,
∵4BD=3CD,
∴CD=
| 4 |
| 3 |
∴点C的坐标为(3,
| 4 |
| 3 |
③∵点C的坐标为(3,
| 4 |
| 3 |
∴k=3×
| 4 |
| 3 |
④设B点横坐标为:x,则其纵坐标为:-
| 3 |
| x |
| 4 |
| x |
则BC=
| 4 |
| x |
| 3 |
| x |
| 7 |
| x |
则△ABC的面积为:
| 1 |
| 2 |
| 7 |
| x |
故选:B.
点评:此题主要考查了反比例函数的性质以及三角形面积等知识,根据题意得出BC的长是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
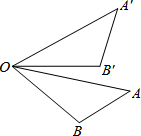 如图,若将△AOB绕点O按逆时针方向旋转44°后,得到△A′OB′,且AO=2,则AA′的长为( )
如图,若将△AOB绕点O按逆时针方向旋转44°后,得到△A′OB′,且AO=2,则AA′的长为( )| A、4sin22° |
| B、2sin44° |
| C、4cos22° |
| D、2cos44° |
 如图所示,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,求∠APD的度数.
如图所示,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,求∠APD的度数. 如图所示,在△ABC中,∠ACB=90°,∠ADC=∠ACD,∠BCE=∠BEC,求∠DCE的度数.
如图所示,在△ABC中,∠ACB=90°,∠ADC=∠ACD,∠BCE=∠BEC,求∠DCE的度数.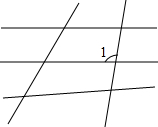 在图中,先标上适当的字母,再回答下列问题;
在图中,先标上适当的字母,再回答下列问题; 如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数y=
如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数y= 如图,△ABD是等腰直角三角形,∠BAD=90°,BC∥AD,BC=2AB,CE平分∠BCD,交AB于E,交BD于H.求证:
如图,△ABD是等腰直角三角形,∠BAD=90°,BC∥AD,BC=2AB,CE平分∠BCD,交AB于E,交BD于H.求证: 如图,落地镜CD直立在地面上,小明在A处看到地面上的物体P的俯角为30°,看到该物体在落地镜CD中像Q的俯角为15°,小明眼睛的高度为1.6m,A,P,C在同一水平面上,若物体高度不计,问物体P离小明有多远?离落地镜有多远?(tan15°=2-
如图,落地镜CD直立在地面上,小明在A处看到地面上的物体P的俯角为30°,看到该物体在落地镜CD中像Q的俯角为15°,小明眼睛的高度为1.6m,A,P,C在同一水平面上,若物体高度不计,问物体P离小明有多远?离落地镜有多远?(tan15°=2- 如图,E,F是?ABCD的对角线AC上两点,且AE=CF,求:DE∥BF.
如图,E,F是?ABCD的对角线AC上两点,且AE=CF,求:DE∥BF.