题目内容
 如图,四边形ABCD是菱形,且∠A=60°,又E,F,G,H分别是菱形各边的中点,联结EH,FG,请判断六边形EBFGDH是一个怎样的图形?并说明你的结论.
如图,四边形ABCD是菱形,且∠A=60°,又E,F,G,H分别是菱形各边的中点,联结EH,FG,请判断六边形EBFGDH是一个怎样的图形?并说明你的结论.考点:中点四边形
专题:
分析:连接BD,结合菱形的性质可证明△ABD和△CBD为等边三角形,可得到HE=GF=
BD,结合条件判断六边形EBFGDH为正六边形.
| 1 |
| 2 |
解答: 解:六边形EBFGDH为正六边形,
解:六边形EBFGDH为正六边形,
证明如下:
如图,连接BD,
∵H、E为AB、AD的中点,
∴HE为△ABD的中位线,
∴HE=
BD,同理可得GF=
BD,
又∵四边形ABCD为菱形,
∴AD=AB,且∠A=60°,
∴△ABD为等边三角形,
∴AD=AB=BD,
∴HE=HD=EB,∠DHE=∠HEB=∠ADC=∠ABC=120°,
同理可得GF=DG=FB,∠FGD=∠GFB=120°,
∴HE=EB=BF=FG=GF=DH,∠DHE=∠HEB=∠EBF=∠BFG=∠FGD=GDH,
∴六边形EBFGDH为正六边形.
 解:六边形EBFGDH为正六边形,
解:六边形EBFGDH为正六边形,证明如下:
如图,连接BD,
∵H、E为AB、AD的中点,
∴HE为△ABD的中位线,
∴HE=
| 1 |
| 2 |
| 1 |
| 2 |
又∵四边形ABCD为菱形,
∴AD=AB,且∠A=60°,
∴△ABD为等边三角形,
∴AD=AB=BD,
∴HE=HD=EB,∠DHE=∠HEB=∠ADC=∠ABC=120°,
同理可得GF=DG=FB,∠FGD=∠GFB=120°,
∴HE=EB=BF=FG=GF=DH,∠DHE=∠HEB=∠EBF=∠BFG=∠FGD=GDH,
∴六边形EBFGDH为正六边形.
点评:本题主要考查菱形的性质,掌握菱形的四边相等、对边相互平行是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
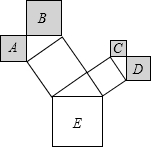 如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是
如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是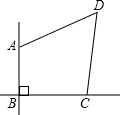 农民牛伯伯承包了一块四边形水稻田ABCD如图,他量得边长AB=90m,BC=120m,CD=130m,DA=140m,且边AB,BC正好位于两条相互垂直的公路的拐角处,请你帮牛伯伯计算一下这块水稻田的面积.
农民牛伯伯承包了一块四边形水稻田ABCD如图,他量得边长AB=90m,BC=120m,CD=130m,DA=140m,且边AB,BC正好位于两条相互垂直的公路的拐角处,请你帮牛伯伯计算一下这块水稻田的面积. 如图,A、B对应的数为-1,-
如图,A、B对应的数为-1,-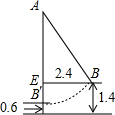 如图是秋千示意图,秋千在平衡位置时,下端B距离地面0.6m,当秋千荡当AB1的位置时,下端B1距离平衡位置的水平距离EB1为2.4m,此时距离地面为1.4m,则秋千AB的长为
如图是秋千示意图,秋千在平衡位置时,下端B距离地面0.6m,当秋千荡当AB1的位置时,下端B1距离平衡位置的水平距离EB1为2.4m,此时距离地面为1.4m,则秋千AB的长为 如图所示,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,求∠APD的度数.
如图所示,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,求∠APD的度数. 已知等腰△ABC中,AB=AC=13,BC=10,求顶角∠A的正弦值.
已知等腰△ABC中,AB=AC=13,BC=10,求顶角∠A的正弦值.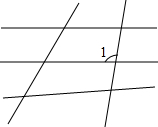 在图中,先标上适当的字母,再回答下列问题;
在图中,先标上适当的字母,再回答下列问题;