题目内容
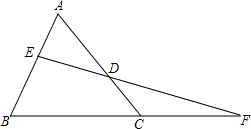如图，在△ABC（AC＞AB）的边AB、AC上分别取点E、D，使BE=CD，连接ED并延长交BC的延长线于点F，判断AB：AC=FD：EF是否成立．考点：相似三角形的判定与性质
专题：探究型
分析：过点E作EH∥AC交BC于点H，即可证到△FDC∽△FEH，△BAC∽△BEH，然后运用相似三角形的性质可得
=
，
=
，再根据条件DC=BE就可得到AB：AC=FD：EF．
| FD |
| EF |
| DC |
| EH |
| AB |
| AC |
| BE |
| EH |
解答：
解：AB：AC=FD：EF
理由：过点E作EH∥AC交BC于点H，如图．
∵EH∥AC，
∴△FDC∽△FEH，△BAC∽△BEH，
∴
=
，
=
．
∵DC=BE，
∴
=
，即AB：AC=FD：EF．
解：AB：AC=FD：EF理由：过点E作EH∥AC交BC于点H，如图．
∵EH∥AC，
∴△FDC∽△FEH，△BAC∽△BEH，
∴
| FD |
| EF |
| DC |
| EH |
| AB |
| AC |
| BE |
| EH |
∵DC=BE，
∴
| FD |
| EF |
| AB |
| AC |
点评：本题主要考查了相似三角形的判定与性质，添加平行线构造相似三角形是解决本题的关键．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
方程x（x+4）=x+4的解为（ ）
| A、x=1 |
| B、x=-4 |
| C、x1=1，x2=-4 |
| D、x1=-1，x2=4 |
已知∠ABM=90°，AB=AC，过点A作AG丄BC，垂足为G，延长AG交BM于点，过点A作AN∥BM，过点C作EF∥AD，与射线AN、BM分别相交于点F、E 
如图，A、B对应的数为-1，-
如图所示，在矩形ABCD中，两个阴影部分是矩形和平行四边形，依照图中的数据，求图中空白部分的面积．
如图所示，在正方形ABCD内有一点P，PA=1，PD=2，PC=3，求∠APD的度数．
如图，将一副三角尺如图所示叠放在一起，则
如图，矩形ABCD的对角线相交于点O，BE⊥AC于点E，EB的延长线与∠ADC的角平线相交于点F，DF交AC于点M，求证：AC=BF．
如图，△P1OA1、△P2A1A2是等腰直角三角形，点P1、P2在函数y=