题目内容
 如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向B以每秒2的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以每秒4的速度移动(不与点C重合),如果P,Q分别从A,B同时出发ts后,四边形APQC的面积为S.
如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向B以每秒2的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以每秒4的速度移动(不与点C重合),如果P,Q分别从A,B同时出发ts后,四边形APQC的面积为S.(1)求S关于t的函数关系式;
(2)多少秒后四边形APQC的面积为△ABC的
| 3 |
| 4 |
考点:一元二次方程的应用,根据实际问题列二次函数关系式
专题:几何动点问题
分析:(1)根据四边形APQC的面积=三角形ABC的面积-三角形PBQ的面积即可得到S关于t的函数关系式;
(2)根据等量关系四边形APQC的面积为△ABC的
,列出方程求解即可.
(2)根据等量关系四边形APQC的面积为△ABC的
| 3 |
| 4 |
解答:解:(1)依题意有
S=
×24×12-
×(12-2t)×4t
=4t2-24t+144,
故S关于t的函数关系式为S=4t2-24t+144;
(2)依题意有
4t2-24t+144=
×
×24×12,
解得t1=t2=3.
故3秒后四边形APQC的面积为△ABC的
.
S=
| 1 |
| 2 |
| 1 |
| 2 |
=4t2-24t+144,
故S关于t的函数关系式为S=4t2-24t+144;
(2)依题意有
4t2-24t+144=
| 3 |
| 4 |
| 1 |
| 2 |
解得t1=t2=3.
故3秒后四边形APQC的面积为△ABC的
| 3 |
| 4 |
点评:本题考查了一元二次方程的应用.关键是用含时间的代数式准确表示BP和BQ的长度,再根据三角形的面积公式列出一元二次方程,进行求解.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图.D是AB的中点,DE∥BC,AF⊥BC,垂足为F,AF交DE于G,则AG:AF的值为( )
如图.D是AB的中点,DE∥BC,AF⊥BC,垂足为F,AF交DE于G,则AG:AF的值为( )| A、1:2 | B、1:4 |
| C、2:1 | D、4:1 |
 已知∠ABM=90°,AB=AC,过点A作AG丄BC,垂足为G,延长AG交BM于点,过点A作AN∥BM,过点C作EF∥AD,与射线AN、BM分别相交于点F、E
已知∠ABM=90°,AB=AC,过点A作AG丄BC,垂足为G,延长AG交BM于点,过点A作AN∥BM,过点C作EF∥AD,与射线AN、BM分别相交于点F、E 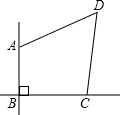 农民牛伯伯承包了一块四边形水稻田ABCD如图,他量得边长AB=90m,BC=120m,CD=130m,DA=140m,且边AB,BC正好位于两条相互垂直的公路的拐角处,请你帮牛伯伯计算一下这块水稻田的面积.
农民牛伯伯承包了一块四边形水稻田ABCD如图,他量得边长AB=90m,BC=120m,CD=130m,DA=140m,且边AB,BC正好位于两条相互垂直的公路的拐角处,请你帮牛伯伯计算一下这块水稻田的面积. 如图,A、B对应的数为-1,-
如图,A、B对应的数为-1,- 如图所示,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,求∠APD的度数.
如图所示,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,求∠APD的度数. 如图所示,在△ABC中,∠ACB=90°,∠ADC=∠ACD,∠BCE=∠BEC,求∠DCE的度数.
如图所示,在△ABC中,∠ACB=90°,∠ADC=∠ACD,∠BCE=∠BEC,求∠DCE的度数.