题目内容
若正方形ABCD的边长为4,对角线交于点O,点E在AC上,且OE=
,延长BE交直线AD于点F,则DF的长为 .
| 2 |
考点:相似三角形的判定与性质,正方形的性质
专题:分类讨论
分析:如图1,首先求出AC的长度,进而得到AE、CE的长度;证明△AEF∽△CEB,列出比例式
=
,求出AF的长;如图2,类比(1)中的解法,求出AF的长度,即可解决问题.
| AF |
| BC |
| AE |
| CE |
解答: 解:如图1,∵四边形ABCD为正方形,
解:如图1,∵四边形ABCD为正方形,
∴∠ABC=90°,OA=OB;由勾股定理得:
AC=
=4
,
∴OA=2
,AE=
,EC=3
;
∵AF∥BC,
∴△AEF∽△CEB,
∴
=
,而BC=4,
∴AF=
,DF=4-AF=
.
如图2,当点F在AD的延长线上时,
同理可求:AE=3
,EC=
;
∵AF∥BC,
∴△AEF∽△CEB,
∴
=
,解得:AF=12,DF=8;
综上所述,DF的长为
或8.
故答案为
或8.
 解:如图1,∵四边形ABCD为正方形,
解:如图1,∵四边形ABCD为正方形,∴∠ABC=90°,OA=OB;由勾股定理得:
AC=
| 42+42 |
| 2 |
∴OA=2
| 2 |
| 2 |
| 2 |
∵AF∥BC,
∴△AEF∽△CEB,
∴
| AF |
| BC |
| AE |
| CE |
∴AF=
| 4 |
| 3 |
| 8 |
| 3 |
如图2,当点F在AD的延长线上时,
同理可求:AE=3
| 2 |
| 2 |
∵AF∥BC,
∴△AEF∽△CEB,
∴
| AF |
| BC |
| AE |
| EC |
综上所述,DF的长为
| 4 |
| 3 |
故答案为
| 4 |
| 3 |
点评:该题主要考查了正方形的性质、相似三角形的判定及其性质等几何知识点及其应用问题;解题的关键是根据题意准确作出符合题意的两个图形,灵活运用相似三角形的判定及其性质来分析、解答.

练习册系列答案
相关题目
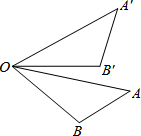 如图,若将△AOB绕点O按逆时针方向旋转44°后,得到△A′OB′,且AO=2,则AA′的长为( )
如图,若将△AOB绕点O按逆时针方向旋转44°后,得到△A′OB′,且AO=2,则AA′的长为( )| A、4sin22° |
| B、2sin44° |
| C、4cos22° |
| D、2cos44° |
 如图所示,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,求∠APD的度数.
如图所示,在正方形ABCD内有一点P,PA=1,PD=2,PC=3,求∠APD的度数. 已知等腰△ABC中,AB=AC=13,BC=10,求顶角∠A的正弦值.
已知等腰△ABC中,AB=AC=13,BC=10,求顶角∠A的正弦值. 如图,矩形ABCD的对角线相交于点O,BE⊥AC于点E,EB的延长线与∠ADC的角平线相交于点F,DF交AC于点M,求证:AC=BF.
如图,矩形ABCD的对角线相交于点O,BE⊥AC于点E,EB的延长线与∠ADC的角平线相交于点F,DF交AC于点M,求证:AC=BF. 如图所示,OB=1,OC=3,AB=AC=4,求点A的坐标.
如图所示,OB=1,OC=3,AB=AC=4,求点A的坐标. 如图所示,在△ABC中,∠ACB=90°,∠ADC=∠ACD,∠BCE=∠BEC,求∠DCE的度数.
如图所示,在△ABC中,∠ACB=90°,∠ADC=∠ACD,∠BCE=∠BEC,求∠DCE的度数. 在图中,先标上适当的字母,再回答下列问题;
在图中,先标上适当的字母,再回答下列问题;