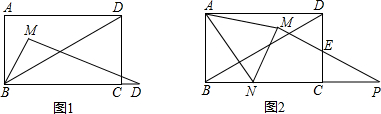题目内容
20.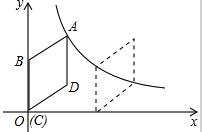 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,菱形ABCD向右平移使点D(4,3)落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则菱形ABCD平移的距离为$\frac{20}{3}$.
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,菱形ABCD向右平移使点D(4,3)落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则菱形ABCD平移的距离为$\frac{20}{3}$.
分析 根据点D的坐标为(4,3),即可得出DE的长以及DO的长,即可得出A点坐标,进而求出k的值,再根据D′F′的长度即可得出D′点的纵坐标,进而利用反比例函数的性质求出OF′的长,即可得出答案.
解答 解:作DE⊥BO,于点E,DF⊥x轴于点F,
∵点D的坐标为(4,3),
∴FO=4,DF=3,
∴DO=5,
∴AD=5,
∴A点坐标为:(4,8),
∴xy=4×8=32,
∴k=32;
∵将菱形ABCD向右平移,使点D落在反比例函数y=$\frac{32}{x}$(x>0)的图象上,
∴DF=3,D′F′=3,
∴D′点的纵坐标为3,
∴3=$\frac{32}{x}$,
解得:x=$\frac{32}{3}$,
∴OF′=$\frac{32}{3}$,
∴FF′=$\frac{32}{3}$-4=$\frac{20}{3}$,
∴菱形ABCD向右平移的距离为:$\frac{20}{3}$.
故答案为:$\frac{20}{3}$.
点评 本题主要考查了反比例函数图象上点的坐标性质以及菱形的性质以及平移的性质,根据已知得出A点坐标是解题关键.

练习册系列答案
相关题目
10.下列图案中既是轴对称又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,等腰△ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最小值为8cm.
如图,等腰△ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最小值为8cm.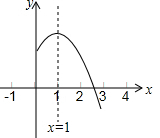 二次函数y=ax2+bx+c的图象的对称轴是直线x=1,其图象的一部分如图所示,下列说法正确的是①②(填正确结论的序号).
二次函数y=ax2+bx+c的图象的对称轴是直线x=1,其图象的一部分如图所示,下列说法正确的是①②(填正确结论的序号).