题目内容
6. 如图,已知线段AB=4,O为AB的中点,P是平面内的-个动点,在运动过程中保持OP=1不变,连结BP,将PB绕点P逆时针旋转90°到PC,连结BC、AC,则线段AC长的取值范围是$\sqrt{2}$≤AC≤3$\sqrt{2}$.
如图,已知线段AB=4,O为AB的中点,P是平面内的-个动点,在运动过程中保持OP=1不变,连结BP,将PB绕点P逆时针旋转90°到PC,连结BC、AC,则线段AC长的取值范围是$\sqrt{2}$≤AC≤3$\sqrt{2}$.
分析 以O为坐标原点建立坐标系,过点C作CD⊥y轴,垂足为D,过点P作PE⊥DC,垂足为E,延长EP交x轴于点F,设点P的坐标为(x,y),则x2+y2=1.然后证明△ECP≌△FPB,由全等三角形的性质得到EC=PF=y,FB=EP=2-x,从而得到点C(x+y,y+2-x),最后依据两点间的距离公式可求得AC的范围.
解答 解:如图所示:过点C作CD⊥y轴,垂足为D,过点P作PE⊥DC,垂足为E,延长EP交x轴于点F.
∵AB=4,O为AB的中点,
∴A(-2,0),B(2,0).
设点P的坐标为(x,y),则x2+y2=1.
∵∠EPC+∠BPF=90°,∠EPC+∠ECP=90°,
∴∠ECP=∠FPB.
由旋转的性质可知:PC=PB.
在△ECP和△FPB中$\left\{\begin{array}{l}{∠ECP=∠FPB}\\{∠PEC=∠PFB}\\{PC=PB}\end{array}\right.$,
∴△ECP≌△FPB.
∴EC=PF=y,FB=EP=2-x.
∴C(x+y,y+2-x).
∵AB=4,O为AB的中点,
∴AC=$\sqrt{(x+y+2)^{2}+(y+2-x)^{2}}$=$\sqrt{2{x}^{2}+2{y}^{2}+8y+8}$.
∵x2+y2=1,
∴AC=$\sqrt{10-8y}$.
∵-1≤y≤1,
∴$\sqrt{2}$≤AC≤3$\sqrt{2}$.
故答案为:$\sqrt{2}$≤AC≤3$\sqrt{2}$.
点评 本题主要考查的是旋转的性质、全等三角形的性质和判定,两点间的距离公式的应用,列出AC的长度与点P的坐标之间的关系式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
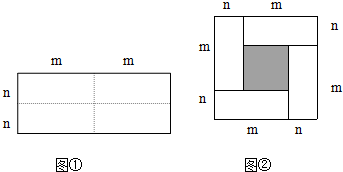
16.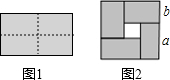 如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积为( )
如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积为( )
 如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积为( )
如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积为( )| A. | ab | B. | (a+b)2 | C. | (a-b)2 | D. | a2-b2 |
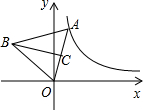 如图,在平面直角坐标系中,点A是双曲线y=$\frac{4}{x}$(x>0)上一动点,以OA为边作等边△AOB,高BC的最小值为$\sqrt{6}$.
如图,在平面直角坐标系中,点A是双曲线y=$\frac{4}{x}$(x>0)上一动点,以OA为边作等边△AOB,高BC的最小值为$\sqrt{6}$.