题目内容
10.如图,4×4方格中每个小正方形的边长为1.(1)求图中正方形ABCD的面积和周长.
(2)利用正方形ABCD,在下面的数轴上表示实数$\sqrt{8}$和-$\sqrt{2}$(保留作图痕迹).

分析 (1)直接利用勾股定理得出正方形的边长,进而得出其面积和周长;
(2)直接利用圆规结合(1)中方法得出答案.
解答 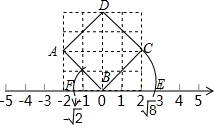 解:(1)如图所示:可得正方形的边长为:$\sqrt{{2}^{2}+{2}^{2}}$=$\sqrt{8}$=2$\sqrt{2}$,
解:(1)如图所示:可得正方形的边长为:$\sqrt{{2}^{2}+{2}^{2}}$=$\sqrt{8}$=2$\sqrt{2}$,
则正方形ABCD的面积为:2$\sqrt{2}$×2$\sqrt{2}$=8,
周长为:2$\sqrt{2}$×4=8$\sqrt{2}$;
(2)如图所示:点E为$\sqrt{8}$的位置,点F是-$\sqrt{2}$的位置.
点评 此题主要考查了复杂作图以及勾股定理等知识,正确应用勾股定理是解题关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
20.某人沿倾斜角为30°的斜坡前进50米,则他上升的最大高度为( )
| A. | 25米 | B. | 25$\sqrt{3}$米 | C. | 20$\sqrt{3}$米 | D. | 25$\sqrt{2}$米 |
1.下列关于x的方程中,一定是一元二次方程的为( )
| A. | x2-2=(x+3)2 | B. | x2-1=0 | C. | x2+$\frac{3}{x}$-5=0 | D. | ax2+bx+c=0 |
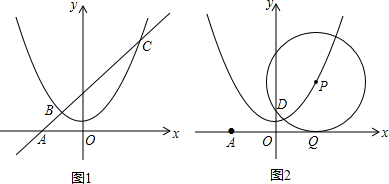
4. 如图,点C是以AB为直径的半圆型铁片上的靠近B点的一个定点,将该铁片按图中的位置斜靠在坐标轴上,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴向x轴正方向滑动,在滑动过程中,点C与原点O距离的变化情况是( )
如图,点C是以AB为直径的半圆型铁片上的靠近B点的一个定点,将该铁片按图中的位置斜靠在坐标轴上,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴向x轴正方向滑动,在滑动过程中,点C与原点O距离的变化情况是( )
 如图,点C是以AB为直径的半圆型铁片上的靠近B点的一个定点,将该铁片按图中的位置斜靠在坐标轴上,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴向x轴正方向滑动,在滑动过程中,点C与原点O距离的变化情况是( )
如图,点C是以AB为直径的半圆型铁片上的靠近B点的一个定点,将该铁片按图中的位置斜靠在坐标轴上,现点A沿着y轴向终点O滑动,同时点B相应地沿着x轴向x轴正方向滑动,在滑动过程中,点C与原点O距离的变化情况是( )| A. | 一直增大 | B. | 保持不变 | C. | 先增大后减小 | D. | 先减小后增大 |
5.已知实数a满足|200-a|+$\sqrt{a-201}$=a,则a-2002的值是( )
| A. | 199 | B. | 200 | C. | 201 | D. | 202 |
 如图,已知圆环的外圆半径为46mm,内圆半径为27mm,求圆环的面积.(π取3.14,结果保留2个有效数字)
如图,已知圆环的外圆半径为46mm,内圆半径为27mm,求圆环的面积.(π取3.14,结果保留2个有效数字)