题目内容
4.已知x2+y2-6x+4y+13=0,求(2x-y)2-2(2x-y)(x+2y)+(x+2y)2的值.分析 根据偶次方的非负性即可得出x=3、y=-2,利用完全平方公式将(2x-y)2-2(2x-y)(x+2y)+(x+2y)2变形为(x+y)2,再代入x、y的值即可得出结论.
解答 解:∵x2+y2-6x+4y+13=(x-3)2+(y+2)2=0,
∴x-3=0,y+2=0,
∴x=3,y=-2,
∴(2x-y)2-2(2x-y)(x+2y)+(x+2y)2=[(2x-y)-(x-2y)]2=(x+y)2=(3-2)2=1.
点评 本题考查了配方法的应用、偶次方的非负性以及整式的混合运算,根据偶次方的非负性找出x、y的值是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
19.“十一”黄金周期间,云南野生动物园在7天假期中每天旅游的人数变化如表:(正数表示比前一天多的人数,负数表示比前一天少的人数)
(1)若9月30目的游客人数记为a万人,请用含a的式子表示10月2日的游客人数;
(2)在(1)的条件下,请判断7天内游客人数最多的是哪天?游客人数是多少?
(3)若9月30日的游客人数为2万人,门票每人10元,问黄金周期间云南野生动物园门票的收入是多少元?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 (单位:万人) | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)在(1)的条件下,请判断7天内游客人数最多的是哪天?游客人数是多少?
(3)若9月30日的游客人数为2万人,门票每人10元,问黄金周期间云南野生动物园门票的收入是多少元?
14.从2开始,连续的偶数相加,它们和的情况如表:
(1)如果n=8时,那么S的值为72
(2)根据表中的规律猜想:用n的代数式表示S的公式为S=2+4+56+8+…+2n=n(n+1);
(3)根据上题的规律计算300+302+304+…+2004+2006的值(要有计算过程)
| 加数的个数n | 连续偶数的和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
(2)根据表中的规律猜想:用n的代数式表示S的公式为S=2+4+56+8+…+2n=n(n+1);
(3)根据上题的规律计算300+302+304+…+2004+2006的值(要有计算过程)
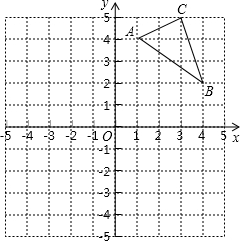 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).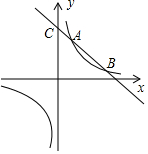 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(1,5)和点B,与y轴相交于点C(0,6).
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(1,5)和点B,与y轴相交于点C(0,6).