题目内容
9.解不等式组$\left\{\begin{array}{l}x-3({x-2})≤8\\ x-\frac{1+2x}{3}<1\end{array}\right.$,并把解集表示在数轴上.分析 根据不等式的性质分别求出每个不等式的解集,根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{x-3(x-2)≤8①}\\{x-\frac{1+2x}{3}<1②}\end{array}\right.$,
由不等式①得:x≥-1,
由不等式②得:x<2,
∴不等式组的解集是-1≤x<2,
在数轴上表示不等式组的解集为: .
.
点评 本题考查了不等式的性质和解一元一次不等式(组)的应用,关键是根据不等式的解集找出不等式组的解集,题目比较好,难度也不大.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 如图所示,已知EF∥AD,∠1=∠2,∠BAC=70°,你能求出∠AGD的度数吗?
如图所示,已知EF∥AD,∠1=∠2,∠BAC=70°,你能求出∠AGD的度数吗?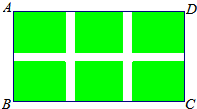 如图,小区规划在一个长80m,宽40m的长方形场地上修建三条同样宽的通道,使其中两条与DC平行,另一条与BC平行,场地的其余部分种草,通道的宽度为x m.
如图,小区规划在一个长80m,宽40m的长方形场地上修建三条同样宽的通道,使其中两条与DC平行,另一条与BC平行,场地的其余部分种草,通道的宽度为x m. 如图,把一个正方形纸片对折两次,然后沿图中虚线剪下一个角,若打开后得到一个正方形纸片,则剪切线与折痕所成的角α的度数等于45°.
如图,把一个正方形纸片对折两次,然后沿图中虚线剪下一个角,若打开后得到一个正方形纸片,则剪切线与折痕所成的角α的度数等于45°.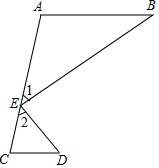 如图,AB∥CD,∠1=∠B,∠2=∠D,A、E、C在同一直线上,试求BE和ED的位置关系,并说明理由.
如图,AB∥CD,∠1=∠B,∠2=∠D,A、E、C在同一直线上,试求BE和ED的位置关系,并说明理由. 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.