题目内容
16. 如图,在△ABC中,∠ACB=90°,BD是△ABC的一条角平分线,DE⊥AB,垂足E,BC=6,AE=2,则AB=8.
如图,在△ABC中,∠ACB=90°,BD是△ABC的一条角平分线,DE⊥AB,垂足E,BC=6,AE=2,则AB=8.
分析 根据角平分线的性质得到DC=DE,根据全等三角形的性质得到BE=BC=6,于是得到结论.
解答 解:∵∠ACB=90°,BD是△ABC的一条角平分线,DE⊥AB,
∴DC=DE,
在Rt△BED与Rt△BED中,$\left\{\begin{array}{l}{DE=DC}\\{BD=BD}\end{array}\right.$,
∴△BED≌△BCD,
∴BE=BC=6,
∵AE=2,
∴AB=8,
故答案为:8.
点评 本题考查了角平分线的性质,全等三角形的性质和判定,熟练掌握全等三角形的判定与性质是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
5.结合创建“全国文明城区”活动,我区某中学以班为单位进行知识竞赛,抽取各班学号分别为5,10,15的三名学生组成班级代表队参赛,统计各班竞赛成绩,绘制成统计图.请结合图中信息,如下结论错误的是( )
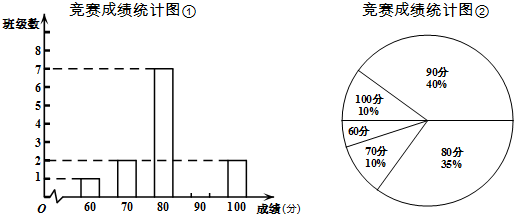

| A. | 这次竞赛各班平均成绩是84 | |
| B. | 这次各班成绩组成的一组数据中的中位数是85 | |
| C. | 这次各班成绩组成的一组数据中的极差是40 | |
| D. | 这次各班成绩组成的一组数据中的众数是80 |
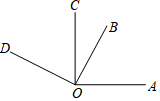 如图,CO⊥AO,DO⊥BO,∠BOC=30°,则∠AOD=150°.
如图,CO⊥AO,DO⊥BO,∠BOC=30°,则∠AOD=150°.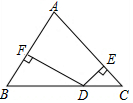 如图,在△ABC中,∠B=63°,∠C=45°,DE⊥AC于E,DF⊥AB于F,那么∠EDF=108°.
如图,在△ABC中,∠B=63°,∠C=45°,DE⊥AC于E,DF⊥AB于F,那么∠EDF=108°.