题目内容
6.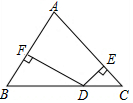 如图,在△ABC中,∠B=63°,∠C=45°,DE⊥AC于E,DF⊥AB于F,那么∠EDF=108°.
如图,在△ABC中,∠B=63°,∠C=45°,DE⊥AC于E,DF⊥AB于F,那么∠EDF=108°.
分析 根据垂线的定义结合三角形内角和定理,可求出∠BDF、∠CDE的度数,再根据∠BDF+∠EDF+∠CDE=180°可求出∠EDF的度数.
解答 解:∵DE⊥AC,DF⊥AB,
∴∠BFD=∠CED=90°,
∴∠BDF=180°-∠B-∠BFD=27°,∠CDE=180°-∠C-∠CED=45°.
∵∠BDF+∠EDF+∠CDE=180°,
∴∠EDF=180°-∠BDF-∠CDE=108°.
故答案为:108°.
点评 本题考查了三角形内角和定理以及垂直,利用三角形内角和定理求出∠BDF、∠CDE的度数是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
14.在平面直角坐标系中,有二次函数y=x2的图象向下平移3个单位,所得图象的解析式为( )
| A. | y=(x-3)2 | B. | y=x2+3 | C. | y=(x+3)2 | D. | y=x2-3 |
1.列方程解应用题
(1)∠α与∠β互为补角,并且∠β的一半比∠α小30°,求∠α、∠β的度数;
(2)若一辆汽车匀速行驶,有一天途径王家庄、青山、秀水三地的时间如表所示,翠湖在青山、秀水两地之间,距青山60千米,距秀水70千米,王家庄到翠湖的路程有多远?
(1)∠α与∠β互为补角,并且∠β的一半比∠α小30°,求∠α、∠β的度数;
(2)若一辆汽车匀速行驶,有一天途径王家庄、青山、秀水三地的时间如表所示,翠湖在青山、秀水两地之间,距青山60千米,距秀水70千米,王家庄到翠湖的路程有多远?
| 地名 | 时间 |
| 王家庄 | 9:00 |
| 青山 | 12:00 |
| 秀水 | 14:00 |
18.下列等式成立的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\sqrt{8}$=2$\sqrt{2}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=2 |
15. 将一副三角板中的两个直角三角板如图放置,使点A在DE上,BC∥DE,其中∠B=∠ACB=45°,∠D=60°,则∠ACE的度数为( )
将一副三角板中的两个直角三角板如图放置,使点A在DE上,BC∥DE,其中∠B=∠ACB=45°,∠D=60°,则∠ACE的度数为( )
 将一副三角板中的两个直角三角板如图放置,使点A在DE上,BC∥DE,其中∠B=∠ACB=45°,∠D=60°,则∠ACE的度数为( )
将一副三角板中的两个直角三角板如图放置,使点A在DE上,BC∥DE,其中∠B=∠ACB=45°,∠D=60°,则∠ACE的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
16.小明掷一枚质地均匀的硬币连续掷了3次,其中2次正面朝上、1次反面朝上的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
 如图,在△ABC中,∠ACB=90°,BD是△ABC的一条角平分线,DE⊥AB,垂足E,BC=6,AE=2,则AB=8.
如图,在△ABC中,∠ACB=90°,BD是△ABC的一条角平分线,DE⊥AB,垂足E,BC=6,AE=2,则AB=8. 如图,点M是直线AB上一点,∠AMC=52°48′,∠BMD=74°30′,则∠CMD=51°42′.
如图,点M是直线AB上一点,∠AMC=52°48′,∠BMD=74°30′,则∠CMD=51°42′.