题目内容
10.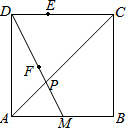 如图,正方形ABCD中,BC=2,点M是边AB的中点,连接DM,DM与AC交于点P,点E在DC上,点F在DP上,且∠DFE=45°.若PF=$\frac{\sqrt{5}}{6}$,则CE=$\frac{7}{6}$.
如图,正方形ABCD中,BC=2,点M是边AB的中点,连接DM,DM与AC交于点P,点E在DC上,点F在DP上,且∠DFE=45°.若PF=$\frac{\sqrt{5}}{6}$,则CE=$\frac{7}{6}$.
分析 如图,连接EF.首先求出DM、DF的长,证明△DEF∽△DPC,可得$\frac{DF}{DC}$=$\frac{DE}{DP}$,求出DE即可解决问题.
解答 解:如图,连接EF.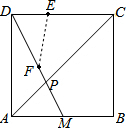
∵四边形ABCD是正方形,
∴AB=BC=CD=DA=2,∠DAB=90°,∠DCP=45°,
∴AM=BM=1,
在Rt△ADM中,DM=$\sqrt{A{D}^{2}+A{M}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∵AM∥CD,
∴$\frac{AM}{DC}$=$\frac{MP}{PD}$=$\frac{1}{2}$,
∴DP=$\frac{2\sqrt{5}}{3}$,∵PF=$\frac{\sqrt{5}}{6}$,
∴DF=DP=PF=$\frac{\sqrt{5}}{2}$,
∵∠EDF=∠PDC,∠DFE=∠DCP,
∴△DEF∽△DPC,
∴$\frac{DF}{DC}$=$\frac{DE}{DP}$,
∴$\frac{\frac{\sqrt{5}}{2}}{2}$=$\frac{DE}{\frac{2\sqrt{5}}{3}}$,
∴DE=$\frac{5}{6}$,
∴CE=CD-DE=2-$\frac{5}{6}$=$\frac{7}{6}$.
故答案为$\frac{7}{6}$.
点评 本题考查正方形的性质、相似三角形的判定和性质、勾股定理、平行线分线段成比例定理等知识,解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
19.在△ABC纸片中,∠ACB=90°,AC=6,BC=8,沿过其中一个顶点的直线把△ABC剪开,若剪得的两个三角形中仅有一个是等腰三角形,那么这个等腰三角形的面积不可能是( )
| A. | 14.4 | B. | 19.2 | C. | 18.75 | D. | 17 |
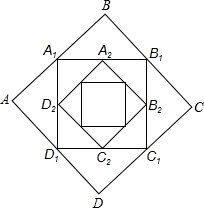 如图,正方形ABCD的边长为2,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第五个正方形A5B5C5D5周长是$\sqrt{2}$.
如图,正方形ABCD的边长为2,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第五个正方形A5B5C5D5周长是$\sqrt{2}$.