题目内容
5.已知一个二次函数的关系式为y=x2-(m+1)x+m.(1)若m=3时,求抛物线顶点坐标:
(2)当-3<x<2时,该二次函数的图象与x轴有且只有一个公共点,求m的取值范围;
(3)若该二次函数的图象与x轴有两个交点A、B,线段AB(含端点)的长不大于2,且m为正常数,求m的值.
分析 (1)代入m=3可得抛物线解析式,即可解题;
(2)易得抛物线与x轴固定有一个交点(1,0),即可解题;
(3)根据抛物线与x轴固定有一个交点(1,0)和AB≤2,即可解题.
解答 解:(1)∵m=3时,二次函数关系式为y=x2-4x+3=(x-2)2-1,
∴抛物线顶点为(2,-1);
(2)化简y=x2-(m+1)x+m得:y=(x-m)(x-1),
∴抛物线与x轴必有一个交点(1,0),
∵-3<x<2时,二次函数的图象与x轴有且只有一个公共点,
∴x=-3时,y=9+3(m+1)+m≤0,解得:m≤-3,
检验得:此时△>0,
∴m≤-3符合题意;
(3)∵化简y=x2-(m+1)x+m得:y=(x-m)(x-1),
∴二次函数的图象与x轴有两个交点(1,0)(m,0),
∵AB≤2,
∴-1≤m≤3,
∵△>0,
∴(m+1)2-4m>0,解得:m≠1,
∴-1≤m<1或1<m≤3.
点评 本题考查了抛物线顶点的计算,考查了二次函数与x轴有两个交点需△>0的性质,本题中求得抛物线与x轴固定有一个交点(1,0)是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
16.下列说法正确的是( )
| A. | 从一个不透明的袋子里面挑球,连续10次都摸出红球,那么袋子里面只有红球 | |
| B. | 天气预报“明天降水概率25%”,是指明天有25%的时间会下雨 | |
| C. | 某种福利彩票,中奖率是千分之一,买这种彩票1000张,一定会中奖 | |
| D. | 连续投一枚硬币,若5次都是正面朝上,则第六次仍然可能正面朝上 |
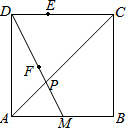 如图,正方形ABCD中,BC=2,点M是边AB的中点,连接DM,DM与AC交于点P,点E在DC上,点F在DP上,且∠DFE=45°.若PF=$\frac{\sqrt{5}}{6}$,则CE=$\frac{7}{6}$.
如图,正方形ABCD中,BC=2,点M是边AB的中点,连接DM,DM与AC交于点P,点E在DC上,点F在DP上,且∠DFE=45°.若PF=$\frac{\sqrt{5}}{6}$,则CE=$\frac{7}{6}$.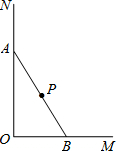 如图,木杆AB斜靠在墙壁上,∠OAB=30°,AB=4米.当木杆的上端A沿墙壁NO下滑时,木杆的底端B也随之沿着地面上的射线OM方向滑动.设木杆的顶端A匀速下滑到点O停止,则木杆的中点P到射线OM的距离y(米)与下滑的时间x(秒)之间的函数图象大致是( )
如图,木杆AB斜靠在墙壁上,∠OAB=30°,AB=4米.当木杆的上端A沿墙壁NO下滑时,木杆的底端B也随之沿着地面上的射线OM方向滑动.设木杆的顶端A匀速下滑到点O停止,则木杆的中点P到射线OM的距离y(米)与下滑的时间x(秒)之间的函数图象大致是( )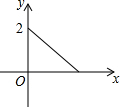
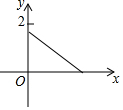

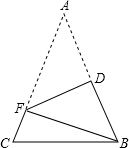 如图,在△ABC中,AB=AC,AB+BC=8,将△ABC折叠,使点A落在点B处,折痕为DF,则△BCF的周长是( )
如图,在△ABC中,AB=AC,AB+BC=8,将△ABC折叠,使点A落在点B处,折痕为DF,则△BCF的周长是( )