题目内容
20.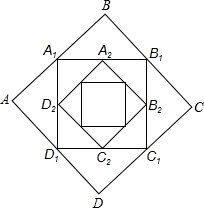 如图,正方形ABCD的边长为2,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第五个正方形A5B5C5D5周长是$\sqrt{2}$.
如图,正方形ABCD的边长为2,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第五个正方形A5B5C5D5周长是$\sqrt{2}$.
分析 根据题意,利用中位线定理可证明顺次连接正方形ABCD四边中点得正方形A1B1C1D1的面积为正方形ABCD面积的一半,根据面积关系可得周长关系,以此类推可得正方形A5B5C5D5的周长.
解答 解:顺次连接正方形ABCD四边的中点得正方形A1B1C1D1,则得正方形A1B1C1D1的面积为正方形ABCD面积的一半,即$\frac{1}{2}$,则周长是原来的$\frac{\sqrt{2}}{2}$;
顺次连接正方形A1B1C1D1中点得正方形A2B2C2D2,则正方形A2B2C2D2的面积为正方形A1B1C1D1面积的一半,即$\frac{1}{4}$,则周长是原来的$\frac{1}{2}$;
顺次连接正方形A2B2C2D2得正方形A3B3C3D3,则正方形A3B3C3D3的面积为正方形A2B2C2D2面积的一半,即$\frac{1}{8}$,则周长是原来的$\frac{\sqrt{2}}{4}$;
…
故第n个正方形周长是原来的$\sqrt{\frac{1}{{2}^{n}}}$,
则第五个正方形A5B5C5D5周长是8×$\sqrt{\frac{1}{{2}^{5}}}$=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查了利用了三角形的中位线的性质,相似图形的面积比等于相似比的平方的性质.进而得到周长关系.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
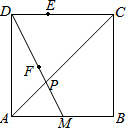 如图,正方形ABCD中,BC=2,点M是边AB的中点,连接DM,DM与AC交于点P,点E在DC上,点F在DP上,且∠DFE=45°.若PF=$\frac{\sqrt{5}}{6}$,则CE=$\frac{7}{6}$.
如图,正方形ABCD中,BC=2,点M是边AB的中点,连接DM,DM与AC交于点P,点E在DC上,点F在DP上,且∠DFE=45°.若PF=$\frac{\sqrt{5}}{6}$,则CE=$\frac{7}{6}$.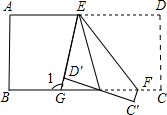 如图,将一张长方形纸片沿EF折叠后,点D、C分别落在点D′、C′的位置,ED′的延长线与BC相交于点G,若∠EFG=50°,则∠1=100°.
如图,将一张长方形纸片沿EF折叠后,点D、C分别落在点D′、C′的位置,ED′的延长线与BC相交于点G,若∠EFG=50°,则∠1=100°.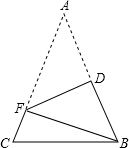 如图,在△ABC中,AB=AC,AB+BC=8,将△ABC折叠,使点A落在点B处,折痕为DF,则△BCF的周长是( )
如图,在△ABC中,AB=AC,AB+BC=8,将△ABC折叠,使点A落在点B处,折痕为DF,则△BCF的周长是( )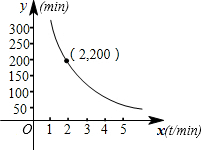 码头工人往一艘轮船上装载货物,装完货物所需时间ymin与装载速度xt/min之间的函数关系如图.
码头工人往一艘轮船上装载货物,装完货物所需时间ymin与装载速度xt/min之间的函数关系如图.