题目内容
5.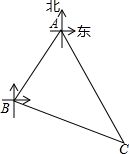 A,B,C三个城市的位置如图所示,城市B在城市A的西南方向(南偏西45°)100km处,城市C在城市A的南偏东30°方向,在城市B的南偏东75°方向.求城市A、C之间的距离.(结果取整数,参考数据:$\sqrt{6}$≈2.45)
A,B,C三个城市的位置如图所示,城市B在城市A的西南方向(南偏西45°)100km处,城市C在城市A的南偏东30°方向,在城市B的南偏东75°方向.求城市A、C之间的距离.(结果取整数,参考数据:$\sqrt{6}$≈2.45)
分析 作AD⊥BC于点D,易知∠ABD=60°、∠BAC=75°,在RT△ABD中AD=AB•sin∠ABD,在RT△ACD中可得∠CAD度数,进而可得AC=$\frac{AD}{cos∠CAD}$.
解答 解:如图,作AD⊥BC于点D,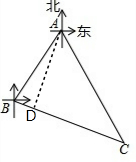
根据题意知,∠ABD=60°,∠BAC=75°,AB=100km,
在RT△ABD中,AD=AB•sin∠ABD=100×$\frac{\sqrt{3}}{2}$=50$\sqrt{3}$(km),
∵∠BAC=75°,∠BAD=30°,
∴∠DAC=45°,
∴在RT△ACD中,AC=$\frac{AD}{cos∠CAD}=\frac{50\sqrt{3}}{\frac{\sqrt{2}}{2}}$=50$\sqrt{6}$≈123(km)
答:城市A、C之间的距离约为123km.
点评 本题主要考查解直角三角形的应用能力,解答此类题目的关键是将三角形转化为含特殊角度的直角三角形,再利用特殊角的三角函数值或勾股定理解答.

练习册系列答案
相关题目
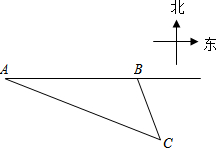 如图,我渔政船在东海海面上自西向东匀速巡航,在A地观测到某海岛C在东偏南21.3°方向上.若渔政船继续向东航行60海里到达B处,此时观测到海岛C在东偏南63.5°方向上.之后,渔政船再向东航多少海里,离海岛C的距离最近?
如图,我渔政船在东海海面上自西向东匀速巡航,在A地观测到某海岛C在东偏南21.3°方向上.若渔政船继续向东航行60海里到达B处,此时观测到海岛C在东偏南63.5°方向上.之后,渔政船再向东航多少海里,离海岛C的距离最近?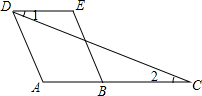 请将下列推理过程补充完整.
请将下列推理过程补充完整.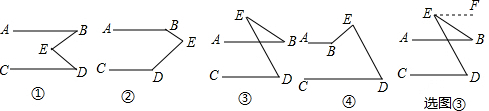
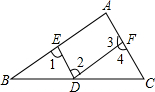 如图,下列条件:①∠1=∠2;②∠A=∠4;③∠1=∠4;④∠A+∠3=180°;⑤∠C=∠BDE,其中能判定AB∥DF的有( )
如图,下列条件:①∠1=∠2;②∠A=∠4;③∠1=∠4;④∠A+∠3=180°;⑤∠C=∠BDE,其中能判定AB∥DF的有( )