题目内容
16.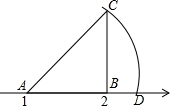 如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )| A. | 1.4 | B. | $\sqrt{2}$ | C. | $\sqrt{2}+1$ | D. | 2.4 |
分析 根据题意运用勾股定理求出AC的长,即可得到答案.
解答 解:在Rt△ABC中,AB=2-1=1,BC=1,
由勾股定理得,AC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
则点D表示的数为$\sqrt{2}$+1.
故选:C.
点评 本题考查的是勾股定理,实数与数轴的关系,正确运用勾股定理求出AC的长是解题的关键,要理解数轴上的点与实数的对应关系.

练习册系列答案
相关题目
4.多项式-$\frac{1}{5}$x|m|+(m-2)x+1是关于x的二次三项式,则m的值是( )
| A. | 2 | B. | -2 | C. | -4 | D. | 2或-2 |
1. 如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=25°,则∠ADE的度数为( )
如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=25°,则∠ADE的度数为( )
 如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=25°,则∠ADE的度数为( )
如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=25°,则∠ADE的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
3. 如图,AE∥DF,AE=DF,则添加下列条件还不能使△EAC≌△FDB的为( )
如图,AE∥DF,AE=DF,则添加下列条件还不能使△EAC≌△FDB的为( )
 如图,AE∥DF,AE=DF,则添加下列条件还不能使△EAC≌△FDB的为( )
如图,AE∥DF,AE=DF,则添加下列条件还不能使△EAC≌△FDB的为( )| A. | AB=CD | B. | CE∥BF | C. | ∠E=∠F | D. | CE=BF |
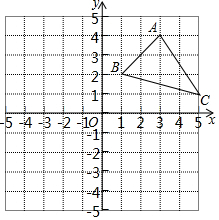 如图,在平面直角坐标系xOy中,有△ABC,请按要求完成下列各问题:
如图,在平面直角坐标系xOy中,有△ABC,请按要求完成下列各问题:
 如图,在平面直角坐标系中,△OAB的顶点A、B的坐标分别为(4,0)、(4,n),若经过点O、A的抛物线y=-x2+bx+c的顶点C落在边OB上,则图中阴影部分图形的面积和为8.
如图,在平面直角坐标系中,△OAB的顶点A、B的坐标分别为(4,0)、(4,n),若经过点O、A的抛物线y=-x2+bx+c的顶点C落在边OB上,则图中阴影部分图形的面积和为8.