题目内容
7.化简求值:已知|m|=$\frac{1}{2}$,|n|=$\frac{1}{3}$且mn<0,m+n<0,求-(-3m2n-mn2)-5(mn2+3m2n)的值.
分析 原式去括号合并得到最简结果,利用绝对值的代数意义求出m与n的值,代入计算即可求出值.
解答 解:∵|m|=$\frac{1}{2}$,|n|=$\frac{1}{3}$,mn<0,m+n<0,
∴m=-$\frac{1}{2}$,n=$\frac{1}{3}$,
∴原式=3m2n+mn2-5mn2-15 mn2=-12m2n-4mn2,
当m=-$\frac{1}{2}$,n=$\frac{1}{3}$时,原式=-12m2n-4mn2=-12×(-$\frac{1}{2}$)2×$\frac{1}{3}$-4×(-$\frac{1}{2}$)×($\frac{1}{3}$)2=-1+$\frac{2}{9}$=-$\frac{7}{9}$.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
18.直角三角形的两直角边长分别为3cm、4cm以直角顶点为圆心,2.4cm长为半径的圆与斜边的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 无法确定 |
16.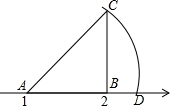 如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
 如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )| A. | 1.4 | B. | $\sqrt{2}$ | C. | $\sqrt{2}+1$ | D. | 2.4 |
14.下面结论中正确的是( )
| A. | 2m+2n=2m+n | B. | 00=0 | C. | 2m•2n=2mn | D. | $\frac{2^n}{3^n}={(\frac{2}{3})^n}$ |
 如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=$\frac{10}{3}$或10s时,△POQ是等腰三角形.
如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=$\frac{10}{3}$或10s时,△POQ是等腰三角形.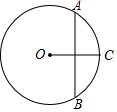 如图,在半径为10的⊙O中,垂直平分半径的弦AB的长为$10\sqrt{3}$.
如图,在半径为10的⊙O中,垂直平分半径的弦AB的长为$10\sqrt{3}$.