题目内容
1. 如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=25°,则∠ADE的度数为( )
如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=25°,则∠ADE的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
分析 根据直角三角形两锐角互余求出∠B,再根据翻折变换的性质可得∠CED=∠B,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答 解:∵∠ACB=90°,∠A=25°,
∴∠B=90°-25°=65°,
∵将△CBD沿CD折叠点B恰好落在AC边上的点E处,
∴∠CED=∠B=65°,
由三角形的外角性质得,∠ADE=∠CED-∠A=65°-25°=40°.
故选C.
点评 本题考查了翻折变换的性质,直角三角形两锐角互余的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
16.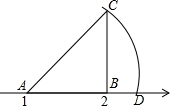 如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
 如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )| A. | 1.4 | B. | $\sqrt{2}$ | C. | $\sqrt{2}+1$ | D. | 2.4 |
10.一个口袋中有4个白球,1个红球,7个黄球,每个球除颜色外其余完全相同,搅匀后随机从袋中摸出1个球,则摸出的球是白球的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{7}{12}$ | D. | $\frac{4}{7}$ |
 阅读下面材料:
阅读下面材料: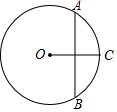 如图,在半径为10的⊙O中,垂直平分半径的弦AB的长为$10\sqrt{3}$.
如图,在半径为10的⊙O中,垂直平分半径的弦AB的长为$10\sqrt{3}$.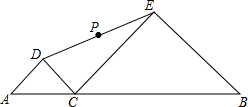 如图,线段AB长为6cm,点C是线段AB上一动点(不与A,B重合),分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1cm处沿AB向右运动至距离B点1cm处时,点P运动的路径长是2cm.
如图,线段AB长为6cm,点C是线段AB上一动点(不与A,B重合),分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1cm处沿AB向右运动至距离B点1cm处时,点P运动的路径长是2cm. 如图,△ABC中,∠C=90°,AD平分∠BAC,CD=2,则点D到AB的距离是2.
如图,△ABC中,∠C=90°,AD平分∠BAC,CD=2,则点D到AB的距离是2.