题目内容
6.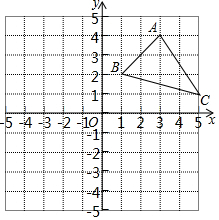 如图,在平面直角坐标系xOy中,有△ABC,请按要求完成下列各问题:
如图,在平面直角坐标系xOy中,有△ABC,请按要求完成下列各问题:(1)写出A、B、C三点的坐标;
(2)△ABC沿X轴方向向左平移6个单位长度后得到△A1B1C1,作出△A1B1C1,并写出A1,B1,C1的坐标.
(3)作出△A1B1C1关于x轴对称的△A2B2C2.
分析 (1)根据图形写出A、B、C三点的坐标;
(2)根据图形平移的性质作出平移后的△A1B1C1,并写出A1,B1,C1的坐标即可;
(3)作出各点关于x轴的对称点,再顺次连接作出△A1B1C1关于x轴对称的△A2B2C2.
解答 解:(1)A(3,4)、B(1,2)、C(5,1);
(2)如图所示:A1(-3,4),B1(-5,2),C1(-1,1);
(3)如图所示:
点评 本题考查的是作图-平移变换,作图-轴对称变换,熟知平移变换的性质/轴对称的性质是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.方程$\frac{x}{4}$=-$\frac{1}{2}$x+3的解为( )
| A. | x=4 | B. | x=$\frac{9}{4}$ | C. | x=-4 | D. | x=$\frac{3}{2}$ |
18.直角三角形的两直角边长分别为3cm、4cm以直角顶点为圆心,2.4cm长为半径的圆与斜边的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 无法确定 |
16.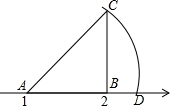 如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
 如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )| A. | 1.4 | B. | $\sqrt{2}$ | C. | $\sqrt{2}+1$ | D. | 2.4 |
 阅读下面材料:
阅读下面材料: 如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=$\frac{10}{3}$或10s时,△POQ是等腰三角形.
如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=$\frac{10}{3}$或10s时,△POQ是等腰三角形.