题目内容
2. 如图,在平面直角坐标系中,△OAB的顶点A、B的坐标分别为(4,0)、(4,n),若经过点O、A的抛物线y=-x2+bx+c的顶点C落在边OB上,则图中阴影部分图形的面积和为8.
如图,在平面直角坐标系中,△OAB的顶点A、B的坐标分别为(4,0)、(4,n),若经过点O、A的抛物线y=-x2+bx+c的顶点C落在边OB上,则图中阴影部分图形的面积和为8.
分析 由条件可求得对称轴,则可求得抛物线解析式,根据抛物线抛物线y=-x2+bx+c的对称性得出阴影部分的面积实际是△ABC的面积,再根据S△ABC=$\frac{1}{2}$S△AOB,由此即可求出阴影部分的面积.
解答 解:
∵抛物线过O、A,
∴c=0,且对称轴为x=2,即-$\frac{b}{-2}$=2,解得b=4,
∴抛物线解析式为y=-x2+4x=-(x-2)2+4,
∴C(2,4),
∵抛物线图象关于直线x=2对称,
∴阴影部分的面积的和实际是△ABC的面积,
∴图中阴影部分的面积的和=$\frac{1}{2}$S△OAB=S△AOC=$\frac{1}{2}$×4×4=8,
故答案为:8.
点评 本题主要考查二次函数的性质,由条件求得抛物线解析式是解题的关键,注意抛物线对称性的应用.

练习册系列答案
相关题目
16.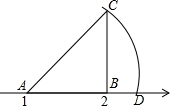 如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
 如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )| A. | 1.4 | B. | $\sqrt{2}$ | C. | $\sqrt{2}+1$ | D. | 2.4 |
10.一个口袋中有4个白球,1个红球,7个黄球,每个球除颜色外其余完全相同,搅匀后随机从袋中摸出1个球,则摸出的球是白球的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{7}{12}$ | D. | $\frac{4}{7}$ |
14.下面结论中正确的是( )
| A. | 2m+2n=2m+n | B. | 00=0 | C. | 2m•2n=2mn | D. | $\frac{2^n}{3^n}={(\frac{2}{3})^n}$ |
11.64的算术平方根是( )
| A. | ±8 | B. | 8 | C. | -8 | D. | $\sqrt{8}$ |
12.一列客车已晚点6分钟,如果将速度每小时加快10km,那么继续行驶20km便可正点运行,如果设客车原来行驶的速度是xkm/h.可列出分式方程为( )
| A. | $\frac{20}{x}$-$\frac{20}{x+10}$=6 | B. | $\frac{20}{x+10}$-$\frac{20}{x}$=6 | C. | $\frac{20}{x}$-$\frac{20}{x+10}$=$\frac{1}{10}$ | D. | $\frac{20}{x+10}$-$\frac{20}{x}$=$\frac{1}{10}$ |
 如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=$\frac{10}{3}$或10s时,△POQ是等腰三角形.
如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=$\frac{10}{3}$或10s时,△POQ是等腰三角形. 如图,△ABC中,∠C=90°,AD平分∠BAC,CD=2,则点D到AB的距离是2.
如图,△ABC中,∠C=90°,AD平分∠BAC,CD=2,则点D到AB的距离是2.