题目内容
19.阅读下列因式分解的过程,再回答所提出的问题:1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]=(1+x)2(1+x)=(1+x)3
(1)上述分解因式的方法是提取公因式法,共应用了2次.
(2)若分解1+x+x(x+1)+x(x+1)2+…+x(x+1)2004,则需应用上述方法2004次,结果是(1+x)2005.
分析 (1)根据提取公因式法分解因式的特点解答;
(2)根据题目信息提取公因式(x+1),整理即可得解.
解答 解:(1)上述分解因式的方法是提取公因式法,共应用了2次.
故答案为:提取公因式法,2;
(2)若分解1+x+x(x+1)+x(x+1)2+…+x(x+1)2004,
则需应用上述方法2004次,结果是:(1+x)2005.
故答案为:2004,(1+x)2005.
点评 本题考查了提公因式法分解因式的推广,要认真观察已知所给的过程,弄清每一步的理由,就可进一步推广.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
10.设a,b,c△ABC的三边长,则$\sqrt{(a+b-c)^{2}}$+|a-b-c|=( )
| A. | 2a-2c | B. | 2b | C. | 2c-2a | D. | 2a+2b |
14.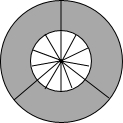 如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )
如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )
 如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )
如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )| A. | 平移一次形成的 | |
| B. | 平移两次形成的 | |
| C. | 以轴心为旋转中心,旋转120°后形成的 | |
| D. | 以轴心为旋转中心,旋转120°、240°后形成的 |
4.二元一次方程2x+y=5的正整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
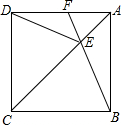 如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.
如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.
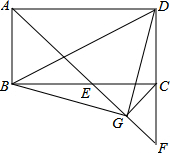 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,点G为EF中点,连接BD、DG.
如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,点G为EF中点,连接BD、DG.