题目内容
8.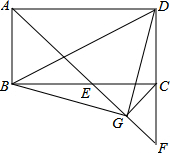 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,点G为EF中点,连接BD、DG.
如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,点G为EF中点,连接BD、DG.(1)试判断△ECF的形状;
(2)连接CG、BG,求证:DG=BG;
(3)求∠BDG的度数.
分析 (1)先证明∠BEA=∠BAE=45°,得出∠CEF=45°,AB=BE,得出∠F=45°,再证出EC=FC,即可得出结论;
(2)先证明∠DCG=∠AEG,再证明△DCG≌△AEG,即可得出结论;
(3)由△DCG≌△AEG,得出∠DGC=∠BGE,证出∠BGD=∠EGC=90°,即可得出结果.
解答 (1)解:△ECF是等腰直角三角形;理由如下:
∵四边形ABCD是矩形,
∴AD∥BC,∠DAB=∠ABC=∠BCD=90°,
∴∠DAE=∠BEA,
∵AE平分∠BAD,
∴∠DAE=∠BAE=45°,
∴∠BEA=∠BAE=45°,
∴∠CEF=45°,AB=BE,
∴∠F=90°-45°=45°,
∴EC=FC,且∠ECF=90°,
∴△ECF是等腰直角三角形;
(2)证明:∵四边形ABCD是矩形,
∴AB=CD,
∵AB=BE,
∴BE=CD,
∵EC=FC,∠ECF=90°,
∴CG=$\frac{1}{2}$EF=EG,∠ECG=$\frac{1}{2}$∠ECF=45°,
∴∠DCG=90°+45°=135°,
∵∠BEG=180°-45°=135°,
∴∠DCG=∠BEG,
在△DCG和△BEG中,$\left\{\begin{array}{l}{CD=BE}&{\;}\\{∠DCG=∠BEG}&{\;}\\{CG=EG}&{\;}\end{array}\right.$,
∴△DCG≌△BEG(SAS),
∴DG=BG;
(3)解:∵△DCG≌△BEG,
∴∠DGC=∠BGE,
∴∠BGD=∠EGC=90°,
∵DG=BG,
∴∠BDG=45°.
点评 本题考查了矩形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握矩形的性质,证明三角形全等和等腰直角三角形是解决问题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 极差 |
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
| A. | x<5 | B. | x>5 | C. | x≥5 | D. | x≤5 |
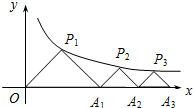 如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点P2015的坐标是($\sqrt{2015}$+$\sqrt{2014}$,$\sqrt{2015}$-$\sqrt{2014}$).
如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点P2015的坐标是($\sqrt{2015}$+$\sqrt{2014}$,$\sqrt{2015}$-$\sqrt{2014}$).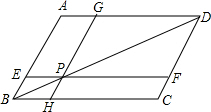 如图,已知?ABCD,点P在对角线BD上,EF∥BC,GH∥AB,点E,H,F,G分别在边AB,BC,CD,AD上,图中哪两个平行四边形的面积相等?试证明你的结论.
如图,已知?ABCD,点P在对角线BD上,EF∥BC,GH∥AB,点E,H,F,G分别在边AB,BC,CD,AD上,图中哪两个平行四边形的面积相等?试证明你的结论.