题目内容
9.解方程组:(1)$\left\{\begin{array}{l}{\frac{x+1}{3}=2y}\\{2(x+1)-y=11}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2(m+n)-3(m-n)=11}\\{3(m+n)+5(m-n)=-12}\end{array}\right.$.
分析 (1)方程组整理后,利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)方程组整理得:$\left\{\begin{array}{l}{x-6y=-1①}\\{2x-y=9②}\end{array}\right.$,
②-①×2得:11y=11,即y=1,
把y=1代入①得:x=5,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{-m+5n=11①}\\{4m-n=-6②}\end{array}\right.$,
①×4+②得:19n=38,即n=2,
把n=2代入②得:m=-1,
则方程组的解为$\left\{\begin{array}{l}{m=-1}\\{n=2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
18.一次函数y=ax+b,当x<5时,y>7,那么不等式ax+b>7的解集为( )
| A. | x<5 | B. | x>5 | C. | x≥5 | D. | x≤5 |
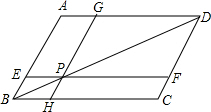 如图,已知?ABCD,点P在对角线BD上,EF∥BC,GH∥AB,点E,H,F,G分别在边AB,BC,CD,AD上,图中哪两个平行四边形的面积相等?试证明你的结论.
如图,已知?ABCD,点P在对角线BD上,EF∥BC,GH∥AB,点E,H,F,G分别在边AB,BC,CD,AD上,图中哪两个平行四边形的面积相等?试证明你的结论.