题目内容
12. 如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )| A. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ |
分析 利用三角形的重心性质得到:AO=$\frac{2}{3}$AD;结合平面向量的三角形法则解答即可.
解答  解:∵在△ABC中,AD是中线,$\overrightarrow{BC}$=$\overrightarrow{b}$,
解:∵在△ABC中,AD是中线,$\overrightarrow{BC}$=$\overrightarrow{b}$,
∴$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{BC}$=$\frac{1}{2}$$\overrightarrow{b}$.
∴$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$.
又∵点O是△ABC的重心,
∴AO=$\frac{2}{3}$AD,
∴$\overrightarrow{AO}$=$\frac{2}{3}$$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$.
故选:B.
点评 此题主要考查了平面向量与重心有关知识,根据重心知识得出AO=$\frac{2}{3}$AD是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
2.一次函数y=-$\frac{3}{2}$x-1的图象不经过的象限是( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
3.下列算式计算正确的是( )
| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | D. | $\sqrt{121÷4}$=$\sqrt{121}$÷$\sqrt{4}$=$\frac{11}{2}$ |
7. 如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是( )
如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是( )
 如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是( )
如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | $\frac{2\sqrt{3}}{3}$ |
1.已知平行四边形ABCD的对角钱AC与BD相交于点O,BD⊥AC,若AB=6,AC=8,则对角线BD的长是( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{2}$ | D. | 4$\sqrt{5}$ |
 如图,在?ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AF的长为2.
如图,在?ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AF的长为2.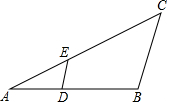 如图,在△ABC中,D、E分别是边AB、AC上的点,如果$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,那么△ADE与△ABC周长的比是1:3.
如图,在△ABC中,D、E分别是边AB、AC上的点,如果$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,那么△ADE与△ABC周长的比是1:3.