题目内容
1.已知平行四边形ABCD的对角钱AC与BD相交于点O,BD⊥AC,若AB=6,AC=8,则对角线BD的长是( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{2}$ | D. | 4$\sqrt{5}$ |
分析 由平行四边形的性质得出OB=OD,OA=OC=$\frac{1}{2}$AC=4,由AC⊥BD,根据勾股定理求出OB,即可得出BD的长.
解答 解:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC=$\frac{1}{2}$AC=4
∵AC⊥BD,
∴由勾股定理得:OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$,
∴BD=2OB=4$\sqrt{5}$.
点评 本题考查了平行四边形的性质、勾股定理;熟练掌握平行四边形的性质,由勾股定理求出OB是解决问题的关键.

练习册系列答案
相关题目
11.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12. 如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
 如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )| A. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ |
9.估计$\sqrt{13}$+1的值在( )
| A. | 2和3之间 | B. | 3和4之间 | C. | 4和5之间 | D. | 5和6之间 |
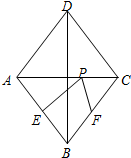 如图,在菱形ABCD中,对角线AC=6,BD=8,点E是边AB的中点,点F、P分别是BC、AC上动点,则PE+PF的最小值是$\frac{24}{5}$.
如图,在菱形ABCD中,对角线AC=6,BD=8,点E是边AB的中点,点F、P分别是BC、AC上动点,则PE+PF的最小值是$\frac{24}{5}$.