题目内容
7. 如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是( )
如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 先根据直角三角形的性质求出AB的长,再由作法可知DE是线段AB的垂直平分线,故可得出BD=AD,BE=AE,再由直角三角形的性质即可得出结论.
解答 解:∵△ABC中,∠C=90°,∠A=30°,BC=2,
∴AB=2BC=4.
∵DE是线段AB的垂直平分线,
∴BD=AD=$\frac{1}{2}$AB=2,BE=AE,
∴∠ABE=∠A=30°,
∴BE=$\frac{BD}{cos30°}$=$\frac{2}{\frac{\sqrt{3}}{2}}$=$\frac{4\sqrt{3}}{3}$.
故选A.
点评 本题考查的是作图-基本作图,熟知线段垂直平分线的作法和直角三角形的性质是解答此题的关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
17.函数y=-2(x-1)2+3的图象的顶点坐标是( )
| A. | (1,-4) | B. | (-1,2) | C. | (-1,3) | D. | (1,3) |
2.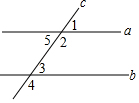 如图,直线a,b被直线c所截,∠1=55°,下列条件能推出a∥b的是( )
如图,直线a,b被直线c所截,∠1=55°,下列条件能推出a∥b的是( )
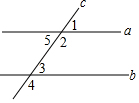 如图,直线a,b被直线c所截,∠1=55°,下列条件能推出a∥b的是( )
如图,直线a,b被直线c所截,∠1=55°,下列条件能推出a∥b的是( )| A. | ∠3=55° | B. | ∠2=55° | C. | ∠4=55° | D. | ∠5=55° |
12. 如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
 如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )| A. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ |
19.一次数学测试,某小组五名同学的成绩如下表所示(有两个数据被遮盖)
那么被遮盖的两个数据依次是( )
| 同学 | A | B | C | D | E | 方差 | 平均成绩 |
| 得分 | 81 | 79 |  | 80 | 82 |  | 80 |
| A. | 78,2 | B. | 78,$\sqrt{2}$ | C. | 80,2 | D. | 80,$\sqrt{2}$ |
17.下列说法中,正确的是( )
| A. | 无理数包括正无理数、零和负无理数 | |
| B. | 无限小数都是无理数 | |
| C. | 正实数包括正有理数和正无理数 | |
| D. | 实数可以分为正实数和负实数两类 |