题目内容
20. 如图,在?ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AF的长为2.
如图,在?ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AF的长为2.
分析 由平行四边形ABCD中,CE平分∠BCD,可证得△BCF是等腰三角形,继而利用AF=BF-AB,求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=8,
∴∠F=∠FCD,
∵CE平分∠BCD,
∴∠BCE=∠FCD,
∴∠F=∠BCE,
∴BF=BC=6,
∴AF=BF-AB=8-6=2;
故答案为:2.
点评 此题考查了平行四边形的性质以及等腰三角形的判定与性质.能证得△BCE是等腰三角形是解此题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
10.从1、3、5、7、9中任取两个数字,组成的两位数是奇数,这是( )
| A. | 必然事件 | B. | 随机事件 | ||
| C. | 不可能事件 | D. | 何类事件不能确定 |
11.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.下列各数是无理数的是( )
| A. | $\sqrt{4}$ | B. | 2.2020020002 | C. | $\root{3}{9}$ | D. | -1 |
12. 如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
 如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )
如图,在△ABC中,中线AD、CE交于点O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为( )| A. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ |
9.估计$\sqrt{13}$+1的值在( )
| A. | 2和3之间 | B. | 3和4之间 | C. | 4和5之间 | D. | 5和6之间 |
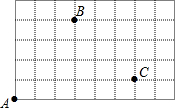 如图,每个小正方格都是边长为1个单位长度的正方形,如果用(0,0)表示A点的位置,用(3,4)表示B点的位置,那么C点的位置可表示为(6,1).
如图,每个小正方格都是边长为1个单位长度的正方形,如果用(0,0)表示A点的位置,用(3,4)表示B点的位置,那么C点的位置可表示为(6,1).