题目内容
2．请写出二元一次方程3x+y=7在正整数范围内的所有解：$\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$、$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$．分析 把x看做已知数表示出y，确定出正整数解即可．
解答 解：方程整理得：y=-3x+7，
当x=1时，y=4；x=2时，y=1，
则方程的正整数解为$\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$、$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$．
故答案为：$\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$、$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$
点评 此题考查了解二元一次方程，解题的关键是将一个未知数看做已知数求出另一个未知数．
练习册系列答案
相关题目
12．
如图，在△ABC中，中线AD、CE交于点O，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为（ ）
如图，在△ABC中，中线AD、CE交于点O，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，那么向量$\overrightarrow{AO}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为（ ）| A． | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B． | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C． | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D． | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ |
17．下列说法中，正确的是（ ）
| A． | 无理数包括正无理数、零和负无理数 | |
| B． | 无限小数都是无理数 | |
| C． | 正实数包括正有理数和正无理数 | |
| D． | 实数可以分为正实数和负实数两类 |
7．
如图所示，a∥b，∠2是∠1的3倍，则∠2等于（ ）
如图所示，a∥b，∠2是∠1的3倍，则∠2等于（ ）| A． | 150° | B． | 135° | C． | 90° | D． | 45° |
如图，?ABCD中，∠ABC=60°，点E、F分别在CD和BC的延长线上，AE∥BD，EF⊥BC，AB的长是1，则EF=$\sqrt{3}$．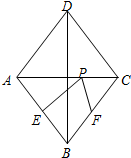
如图，在菱形ABCD中，对角线AC=6，BD=8，点E是边AB的中点，点F、P分别是BC、AC上动点，则PE+PF的最小值是$\frac{24}{5}$．