题目内容
9．如图是用相同的小正方形拼成的图案，第1个图案需1个小正方形，第2个图案需3个小正方形，第3个图案需6个小正方形…，则第n个图案需$\frac{1}{2}$n（n+1）个小正方形．
分析 根据图形的变化发现每增加一个图形其正方形个数分别增加图形的顺序数个，利用发现的规律解答即可．
解答 解：∵第一个图形有1个正方形；
第二个图形有1+2=3个正方形；
第三个图形有1+2+3=6个正方形；
第四个图形有1+2+3+4=10个正方形
…
∴第n个图形有1+2+3+…+n=$\frac{1}{2}$n（n+1）个．
故答案为：$\frac{1}{2}$n（n+1）．
点评 此题考查图形的变化规律，找出图形之间的联系，得出运算规律，解决问题．
练习册系列答案
阅读快车系列答案
相关题目
将连续的偶数2，4，6，8，…排列成如图所示的数表，设中间的数为a，用代数式表示“+”字框内5个数之和为5a．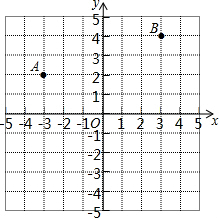
已知两点A（-3，2），B（3，4）．
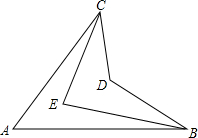如图，若∠ACE=$\frac{1}{3}$∠ACD，∠ABE=$\frac{1}{3}$∠ABD，猜想∠A，∠CEB和∠CDB之间的数量关系为2∠A+∠CDB=3∠CEB．（写出结论，不必证明）
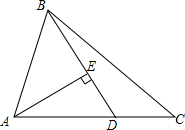如图，△ABC中，∠BCA=45°，点D在AC上，∠BDA=60°，AD=2DC，AE⊥BD于E．求证：
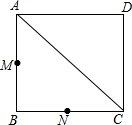如图，四边形ABCD为正方形，M，N分别是AB，BC边的中点，请在对角线AC上找一点P，使PM+PN的值最小（不写作法，保留作图痕迹）．