题目内容
4．
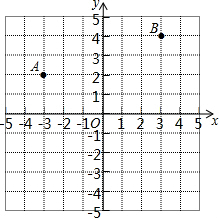已知两点A（-3，2），B（3，4）．（1）在如图所示的坐标系中画出点A和点B；
（2）在x轴上找一点P，使PA+PB最小，并写出P的坐标．
分析 （1）在坐标系中画出A、B点即可；
（2）找出点A关于x轴的对称点A′，连接A′B与x轴交于点P，则P点即为所求，再根据点P在x轴上的位置得出P点坐标即可．
解答 解：（1）如图：
（2）如图所示：P点即为所求点，P（-$\frac{1}{2}$，0）．
点评 本题考查的是轴对称-最短路线问题，熟知“两点之间，线段最短”是解答此题的关键．
练习册系列答案
相关题目
如图，用钢筋做支架，要求BA，DC相交所成的锐角为32°，现测得∠BAC=∠DCA=115°，则这个支架符合设计要求吗？为什么？
13．若一元二次方程x2-mx+n=0无实数根，则抛物线y=-x2+mx-n的图象位于（ ）
| A． | 第一，二，三象限 | B． | x轴上方 | C． | x轴下方 | D． | 第二，三，四象限 |