题目内容
8.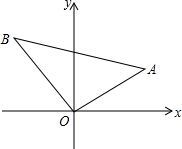 如图,△OAB是等腰直角三角形,AB=4,OA与x轴的夹角为30°,求A、B两点的坐标.
如图,△OAB是等腰直角三角形,AB=4,OA与x轴的夹角为30°,求A、B两点的坐标.
分析 根据已知和勾股定理求出OB、OA,作AC⊥x轴于C,BD⊥x轴于D,根据直角三角形的性质求出AC、OC得到点A的坐标,求出OB、OD得到点B的坐标.
解答 解:作AC⊥x轴于C,BD⊥x轴于D,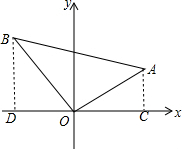
在Rt△ABO中,AB=4,
由勾股定理得,OB2+OA2=AB2,
2OB2=42,
解得;OB=OA=2$\sqrt{2}$,
∵OA=2$\sqrt{2}$,∠AOC=30°,
∴AC=$\frac{1}{2}$OA=$\sqrt{2}$,OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{6}$,
∴点A的坐标为($\sqrt{6}$,$\sqrt{2}$),
∵∠AOB=90°,∠AOC=30°,
∴∠OBD=30°,OB=2$\sqrt{2}$,
∴OD=$\sqrt{2}$,BD=$\sqrt{O{B}^{2}-O{D}^{2}}$=$\sqrt{6}$,
∴点B的坐标为(-$\sqrt{2}$,$\sqrt{6}$).
点评 本题考查的是解直角三角形和坐标与图形性质,掌握锐角三角函数的概念和勾股定理是解题的关键.

练习册系列答案
相关题目
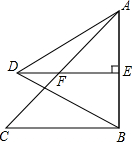 如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,以AB为边向左边作一个等边△ABD,过点D作DE⊥AB于点E,交AC于点F.
如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,以AB为边向左边作一个等边△ABD,过点D作DE⊥AB于点E,交AC于点F.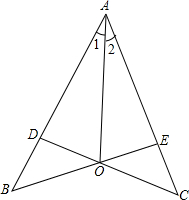 如图,已知∠BEC=∠BDC,BE=CD,求证:∠1=∠2.
如图,已知∠BEC=∠BDC,BE=CD,求证:∠1=∠2.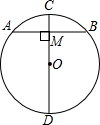 如图.在下列五个条件中:①CD是直径,②CD⊥AB,③AM=BM,④$\widehat{AC}=\widehat{BC}$,③$\widehat{AD}=\widehat{BD}$,只要具备其中两个条件,就可推出其余三个结论.你可以写出相应的命题吗?
如图.在下列五个条件中:①CD是直径,②CD⊥AB,③AM=BM,④$\widehat{AC}=\widehat{BC}$,③$\widehat{AD}=\widehat{BD}$,只要具备其中两个条件,就可推出其余三个结论.你可以写出相应的命题吗?