题目内容
先约分,再求值.
(1)
,其中x=-1;
(2)
,其中x=2;
(3)
,其中a=
,b=-
.
(1)
| 1-4x2 |
| 2x2+x |
(2)
| x2y-2xy+y |
| y-x2y |
(3)
| a2-3ab |
| a2-6ab+9b2 |
| 3 |
| 2 |
| 2 |
| 3 |
考点:分式的化简求值
专题:计算题
分析:(1)原式约分得到最简结果,把x的值代入计算即可求出值;
(2)原式约分得到最简结果,把x的值代入计算即可求出值;
(3)原式约分得到最简结果,把a与b的值代入计算即可求出值.
(2)原式约分得到最简结果,把x的值代入计算即可求出值;
(3)原式约分得到最简结果,把a与b的值代入计算即可求出值.
解答:解:(1)原式=-
=-
,
当x=-1时,原式=-
=-3;
(2)原式=
=-
,
当x=2时,原式=-
;
(3)原式=
=
,
当a=
,b=-
时,原式=
=
.
| (2x+1)(2x-1) |
| x(2x+1) |
| 2x-1 |
| x |
当x=-1时,原式=-
| -2-1 |
| -1 |
(2)原式=
| y(x-1)2 |
| -y(x+1)(x-1) |
| x-1 |
| x+1 |
当x=2时,原式=-
| 1 |
| 3 |
(3)原式=
| a(a-3b) |
| (a-3b)2 |
| a |
| a-3b |
当a=
| 3 |
| 2 |
| 2 |
| 3 |
| ||
|
| 3 |
| 7 |
点评:此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 如图,小明将一张正方形纸片剪去一个宽为3cm的长条后,再从剩下的长方形纸片上剪去一个宽为4cm的长条,如果两次剪下的长条面积正好相等,求原正方形的边长.
如图,小明将一张正方形纸片剪去一个宽为3cm的长条后,再从剩下的长方形纸片上剪去一个宽为4cm的长条,如果两次剪下的长条面积正好相等,求原正方形的边长.
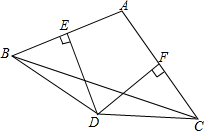 如图,在△ABC中,边AB,AC的垂直平分线相交于点D,垂足分别为E,F.已知∠BAC=100°,∠EDF等于80°,∠ACB=30°,求∠ABD的度数.
如图,在△ABC中,边AB,AC的垂直平分线相交于点D,垂足分别为E,F.已知∠BAC=100°,∠EDF等于80°,∠ACB=30°,求∠ABD的度数. 已知,如图,AB∥CD,∠ABE=135°,∠CDE=80°,则∠BED的度数是
已知,如图,AB∥CD,∠ABE=135°,∠CDE=80°,则∠BED的度数是 如图所示,已知点A、B、C、O分别表示有理数a,b,c,0,试判断下列各式的符号:
如图所示,已知点A、B、C、O分别表示有理数a,b,c,0,试判断下列各式的符号: