题目内容
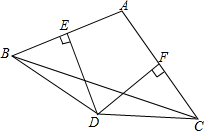 如图,在△ABC中,边AB,AC的垂直平分线相交于点D,垂足分别为E,F.已知∠BAC=100°,∠EDF等于80°,∠ACB=30°,求∠ABD的度数.
如图,在△ABC中,边AB,AC的垂直平分线相交于点D,垂足分别为E,F.已知∠BAC=100°,∠EDF等于80°,∠ACB=30°,求∠ABD的度数.考点:线段垂直平分线的性质
专题:
分析:连接AD,根据线段垂直平分线性质得出BD=AD,AD=CD,求出∠DBA=∠DAB,∠DCA=∠DAC,BD=CD,根据等腰三角形的性质得出∠DBC=∠DCB,设∠DBC=∠DCB=x°,得出方程x+50+30+x=100,求出方程的解即可.
解答:解: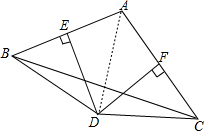 连接AD,
连接AD,
∵边AB,AC的垂直平分线相交于点D,
∴BD=AD,AD=CD,
∴∠DBA=∠DAB,∠DCA=∠DAC,BD=CD,
∴∠DBC=∠DCB,
设∠DBC=∠DCB=x°,
∵∠BAC=100°,∠ACB=30°,
∴∠ABC=50°,
∴x+50+30+x=100,
解得:x=10,
即∠DBC=10°,
∴∠ABD=10°+50°=60°.
 连接AD,
连接AD,∵边AB,AC的垂直平分线相交于点D,
∴BD=AD,AD=CD,
∴∠DBA=∠DAB,∠DCA=∠DAC,BD=CD,
∴∠DBC=∠DCB,
设∠DBC=∠DCB=x°,
∵∠BAC=100°,∠ACB=30°,
∴∠ABC=50°,
∴x+50+30+x=100,
解得:x=10,
即∠DBC=10°,
∴∠ABD=10°+50°=60°.
点评:本题考查了三角形内角和定理,线段垂直平分线性质,等腰三角形的性质的应用,能综合运用性质进行推理是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目
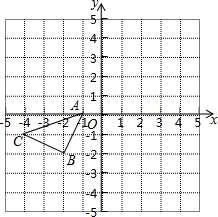 如图所示的正方形网格中,△ABC的顶点A、B、C的坐标分别是(-1,0)、(-2,-2)、(-4,-1).在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点A、B、C的坐标分别是(-1,0)、(-2,-2)、(-4,-1).在所给直角坐标系中解答下列问题: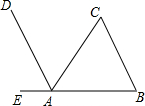 如图,AD∥CB,∠B=60°,∠C=70°,求∠CAE的度数.
如图,AD∥CB,∠B=60°,∠C=70°,求∠CAE的度数.