题目内容
如图,已知AB∥CD,试探究图甲乙中∠A,∠C,∠P三个角之间的数量关系.


考点:平行线的性质
专题:
分析:在图甲中过P作PE∥AB,在图乙中过P作PF∥AB,再利用平行线的性质可得出三个角之间的关系.
解答:解:
如图甲,过P作PE∥AB,

∵AB∥CD,
∴PE∥CD,
∴∠A=∠APE,∠C=∠CPE,
∴∠APC=∠APE+∠CPE=∠A+∠C;
如图乙,过P作PF∥AB,

∵AB∥CD,
∴PF∥CD,
∴∠A+∠APF=∠C+∠CPF=180°,
∴∠A+∠C+∠APF+∠CPF=360°,
即∠A+∠C+∠APC=360°.
如图甲,过P作PE∥AB,

∵AB∥CD,
∴PE∥CD,
∴∠A=∠APE,∠C=∠CPE,
∴∠APC=∠APE+∠CPE=∠A+∠C;
如图乙,过P作PF∥AB,

∵AB∥CD,
∴PF∥CD,
∴∠A+∠APF=∠C+∠CPF=180°,
∴∠A+∠C+∠APF+∠CPF=360°,
即∠A+∠C+∠APC=360°.
点评:本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
化简x(2x-1)-x2(2-x)的结果是( )
| A、-x3-x |
| B、x3-x |
| C、-x2-1 |
| D、x3-1 |
 已知:∠EFB+∠DEF=180°,∠EFB=2∠DEF,FG平分∠AFE.求证:∠AFG=30°.
已知:∠EFB+∠DEF=180°,∠EFB=2∠DEF,FG平分∠AFE.求证:∠AFG=30°.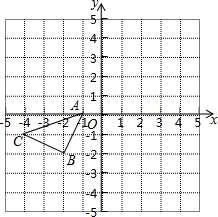 如图所示的正方形网格中,△ABC的顶点A、B、C的坐标分别是(-1,0)、(-2,-2)、(-4,-1).在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点A、B、C的坐标分别是(-1,0)、(-2,-2)、(-4,-1).在所给直角坐标系中解答下列问题: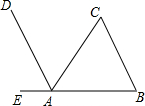 如图,AD∥CB,∠B=60°,∠C=70°,求∠CAE的度数.
如图,AD∥CB,∠B=60°,∠C=70°,求∠CAE的度数.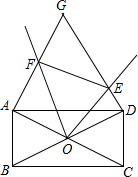 如图所示,矩形ABCD中,对角线AC、BD相交于点O,∠AOD=120°,以AD为边作等边△ADG,在经过点O作∠EOF=60°,与边DG相交于点E,与边AG相交于点F,连接EF.
如图所示,矩形ABCD中,对角线AC、BD相交于点O,∠AOD=120°,以AD为边作等边△ADG,在经过点O作∠EOF=60°,与边DG相交于点E,与边AG相交于点F,连接EF.