题目内容
一个正n边形的边长为a,面积为S,则它的边心距为 .
考点:正多边形和圆
专题:
分析:设边心距为r,根据一个正n边形的边长为a,面积为S可知每个三角形的面积为
,再由三角形的面积公式即可得出结论.
| S |
| n |
解答:解:设边心距为r,
∵正n边形的边长为a,面积为S,
∴每个三角形的面积为
,
∴
=
ar,解得r=
.
故答案为:
.
∵正n边形的边长为a,面积为S,
∴每个三角形的面积为
| S |
| n |
∴
| S |
| n |
| 1 |
| 2 |
| 2S |
| na |
故答案为:
| 2S |
| na |
点评:本题考查的是正多边形和圆,熟记正多边形的定义是解答此题的关键.

练习册系列答案
相关题目
已知B是线段AC上的一点,且BC=
AB,D是AC的中点,若DC=2cm,则AB的长为( )
| 1 |
| 3 |
| A、4cm | ||
| B、3cm | ||
| C、2cm | ||
D、
|
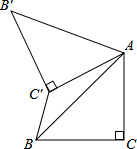 如图,已知△ABC中,∠C=90°,AC=BC=
如图,已知△ABC中,∠C=90°,AC=BC=| 2 |
| A、15° | B、20° |
| C、30° | D、45° |
下列各式成立的是( )
| A、-(-2)2=22 |
| B、(-3)2=6 |
| C、-24=(-2)4 |
| D、(-2)3=-23 |
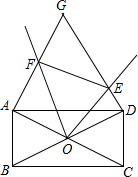 如图所示,矩形ABCD中,对角线AC、BD相交于点O,∠AOD=120°,以AD为边作等边△ADG,在经过点O作∠EOF=60°,与边DG相交于点E,与边AG相交于点F,连接EF.
如图所示,矩形ABCD中,对角线AC、BD相交于点O,∠AOD=120°,以AD为边作等边△ADG,在经过点O作∠EOF=60°,与边DG相交于点E,与边AG相交于点F,连接EF.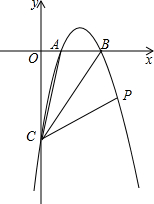 如图:抛物线y=-x2+4x-3与x轴交于A、B两点,与y轴交于C点,点P在抛物线上∠ACB=∠BCP,求P点的坐标.?
如图:抛物线y=-x2+4x-3与x轴交于A、B两点,与y轴交于C点,点P在抛物线上∠ACB=∠BCP,求P点的坐标.?