题目内容
17.二次函数y=ax2+$\frac{3}{2}$x+c(a≠0)的图象交x轴于A,B两点,与y轴交于点C,已知A(-1,0),点C(0,2).(1)求抛物线的解析式,并求出该抛物线的顶点坐标;
(2)若点D是抛物线在第一象限的部分上的一动点,当四边形OCDB的面积最大时,求点D的坐标.
分析 (1)把点A、C的坐标分别代入函数解析式,列出关于系数a、c的方程组,通过解方程组求得它们的值;然后利用配方法把该函数解析式转化为顶点式,易求其顶点坐标;
(2)设出点D的坐标,作ED⊥OC于点D,就可以表示出点D的坐标,从而表示出四边形面积的表达式,利用函数的解析式确定其最值,有最大值则点D存在,就可以求出D点的坐标.
解答  解:(1)把A(-1,0),点C(0,2)分别代入y=ax2+$\frac{3}{2}$x+c,得
解:(1)把A(-1,0),点C(0,2)分别代入y=ax2+$\frac{3}{2}$x+c,得
$\left\{\begin{array}{l}{0=a-\frac{3}{2}+c}\\{2=c}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=2}\end{array}\right.$,
则该函数解析式为:y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2.
因为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-$\frac{1}{2}$(x-$\frac{3}{2}$)2+$\frac{25}{8}$.
所以该抛物线的顶点坐标是($\frac{3}{2}$,$\frac{25}{8}$);
(2)存在.设点D如图所示,过点D作DE⊥OC于点E,
∵A(-1,0),对称轴是x=$\frac{3}{2}$,
∴B(4,0).
设点D的坐标为(a,-$\frac{1}{2}$a2+$\frac{3}{2}$a+2),则E点坐标为(0,-$\frac{1}{2}$a2+$\frac{3}{2}$a+2)
∴EC=-$\frac{1}{2}$a2+$\frac{3}{2}$a+2-2=-$\frac{1}{2}$a2+$\frac{3}{2}$a,DE=a
S四边形OCDB=S梯形OEDB-S△EDC=$\frac{1}{2}$(a+4)(-$\frac{1}{2}$a2+$\frac{3}{2}$a+2)-$\frac{1}{2}$a(-$\frac{1}{2}$a2+$\frac{3}{2}$a)
即S=-a2+4a+4=-(a-2)2+8,
当a=2时,S最大=8,
当a=2时,-$\frac{1}{2}$×4+$\frac{3}{2}$×2+2=3,
∴此时点D的坐标是(2,3).
点评 本题考查了待定系数法求函数的解析式、抛物线与x轴的交点坐标、平面图形的面积的计算,抛物线的顶点式的运用等多个知识点,难度比较大.

 如图,∠AOB=∠BOC,且∠BOC:∠COD:∠DOA=2:5:3,则∠AOB=( )
如图,∠AOB=∠BOC,且∠BOC:∠COD:∠DOA=2:5:3,则∠AOB=( )| A. | 30° | B. | 36° | C. | 40° | D. | 60° |
 在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.
在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.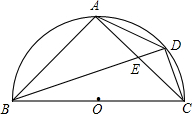 如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC=$\frac{5}{2}$,CD=$\frac{{\sqrt{5}}}{2}$,则sin∠AEB的值为$\frac{2\sqrt{5}}{5}$.
如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC=$\frac{5}{2}$,CD=$\frac{{\sqrt{5}}}{2}$,则sin∠AEB的值为$\frac{2\sqrt{5}}{5}$.