题目内容
 如图,AD为△ABC的中线,分别过点C、B作AD的垂线,垂足分别为E、F.求证:BF=CE.
如图,AD为△ABC的中线,分别过点C、B作AD的垂线,垂足分别为E、F.求证:BF=CE.考点:全等三角形的判定与性质
专题:证明题
分析:由已知条件“过点C、B作AD及其延长线的垂线”易证两个直角相等;再由AD是中线知BD=CD,对顶角∠BDF与∠CDE相等,利用“AAS”来证明△BDF≌△CDE;最后根据全等三角形的对应边相等来证明BF=CE.
解答: 证明:∵CE⊥AF,BF⊥AF,
证明:∵CE⊥AF,BF⊥AF,
∴∠CED=∠BFD=90°,
又∵AD是边BC上的中线,
∴BD=DC;
在Rt△BDF和Rt△CDE中,
∴△BDF≌△CDE(AAS),
∴BF=CE(全等三角形的对应边相等).
 证明:∵CE⊥AF,BF⊥AF,
证明:∵CE⊥AF,BF⊥AF,∴∠CED=∠BFD=90°,
又∵AD是边BC上的中线,
∴BD=DC;
在Rt△BDF和Rt△CDE中,
|
∴△BDF≌△CDE(AAS),
∴BF=CE(全等三角形的对应边相等).
点评:本题考查了全等三角形的判定与性质,关键是通过平行线的判定定理证明CE∥BF,然后通过平行线的性质求得∠DBF=∠DCE才能构建是全等三角形△BDF≌△CDE.

练习册系列答案
相关题目
在△ABC中,O为内心,∠A=70°,则∠BOC=( )
| A、140° | B、135° |
| C、130° | D、125° |
 如图:平行四边形ABCD的对角线AC,BD相交于点O,过O点的直线与AD交于点E,与BC交于点F,试说明:OE=OF.
如图:平行四边形ABCD的对角线AC,BD相交于点O,过O点的直线与AD交于点E,与BC交于点F,试说明:OE=OF. 如图,AC=AD,BC=BD,AB是∠CAD的平分线吗?请说明理由.
如图,AC=AD,BC=BD,AB是∠CAD的平分线吗?请说明理由.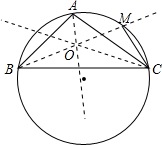 已知点O为△ABC内心,BO的延长线与AC交于N,与△ABC外接圆交于点M,若MC=10,求OM长.
已知点O为△ABC内心,BO的延长线与AC交于N,与△ABC外接圆交于点M,若MC=10,求OM长. 如图,在△ABC中,AD为中线,求证:AB+AC>2AD.
如图,在△ABC中,AD为中线,求证:AB+AC>2AD.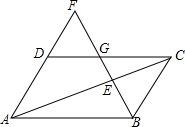 如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE.
如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE. 已知:如图,AB=EF,BC=FD,AD=EC,求证:∠B=∠F.
已知:如图,AB=EF,BC=FD,AD=EC,求证:∠B=∠F. BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是
BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是