题目内容
在平面直角坐标系中,横坐标与纵坐标都是整数的点(x,y)称为整点,如果将二次函数y=x2-6x+
的图象与直线y=-x所围成的封闭图形染成红色,则此红色区域内部及其边界上的整点个数有 个.
| 11 |
| 4 |
考点:二次函数的性质
专题:计算题
分析:先根据方程组组
得到两函数的交点A、B的坐标,再找出从A到B自变量为整数的个数(1、2、3、4),然后把它们分别代入两函数解析式计算出对应的函数值,于是可写出红色区域内部及其边界上的整点的坐标.
|
解答:解:y=x2-6x+
=(x-3)2-
,顶点坐标为(3,-
),
解方程组
得
或
,
所以二次函数y=x2-6x+
的图象与直线y=-x的交点A、B的横坐标分别为
,
),如图,
∵
≤x≤
的整数解为1,2,3,4,
当x=1时,y=-x=-1,y=x2-6x+
=-
,则点(1,-1),(1,-2)满足条件;
当x=2时,y=-x=-2,y=x2-6x+
=-
,则点(2,-2),(2,-3),(2,-4),(2,-5)满足条件;
当x=3时,y=-x=-3,y=x2-6x+
=-
,则点(3,-3),(3,-4),(3,-5),(3,-6)满足条件;
当x=4时,y=-x=-4,y=x2-6x+
=-
,则点(4,-4),(4,-5)满足条件.
故答案为12.
| 11 |
| 4 |
| 25 |
| 4 |
| 25 |
| 4 |

解方程组
|
|
|
所以二次函数y=x2-6x+
| 11 |
| 4 |
5-
| ||
| 2 |
5+
| ||
| 2 |
∵
5-
| ||
| 2 |
5+
| ||
| 2 |
当x=1时,y=-x=-1,y=x2-6x+
| 11 |
| 4 |
| 9 |
| 4 |
当x=2时,y=-x=-2,y=x2-6x+
| 11 |
| 4 |
| 21 |
| 4 |
当x=3时,y=-x=-3,y=x2-6x+
| 11 |
| 4 |
| 25 |
| 4 |
当x=4时,y=-x=-4,y=x2-6x+
| 11 |
| 4 |
| 21 |
| 4 |
故答案为12.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
.学会把求两函数图象的交点问题转化为解方程组的问题.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 如图:平行四边形ABCD的对角线AC,BD相交于点O,过O点的直线与AD交于点E,与BC交于点F,试说明:OE=OF.
如图:平行四边形ABCD的对角线AC,BD相交于点O,过O点的直线与AD交于点E,与BC交于点F,试说明:OE=OF.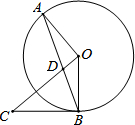 如图,AB为⊙O的弦,BC是⊙O的切线,切点为B,连接CO交AB于点D,BC=DC,请判断OA与OC的位置关系,并说明理由.
如图,AB为⊙O的弦,BC是⊙O的切线,切点为B,连接CO交AB于点D,BC=DC,请判断OA与OC的位置关系,并说明理由.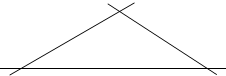 如图,有三条交叉的公路,现要在三条公路交叉所形成的区域内建一货运站,使得货运站到三条公路的路程一样长,请问如何确定货运站的位置?(保留作图痕迹) 简单叙述你的方法.
如图,有三条交叉的公路,现要在三条公路交叉所形成的区域内建一货运站,使得货运站到三条公路的路程一样长,请问如何确定货运站的位置?(保留作图痕迹) 简单叙述你的方法. 如图,AC=AD,BC=BD,AB是∠CAD的平分线吗?请说明理由.
如图,AC=AD,BC=BD,AB是∠CAD的平分线吗?请说明理由.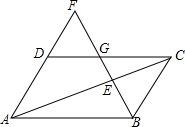 如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE.
如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE.