题目内容
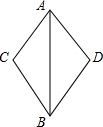 已知:如图,AC=AD,AB是∠CAD的角平分线.求证:BC=BD.
已知:如图,AC=AD,AB是∠CAD的角平分线.求证:BC=BD.考点:全等三角形的判定与性质
专题:证明题
分析:由题干可知AC=AD,再根据角平分线的性质可得∠CAB=∠DAB,再根据AB=AB,即可证明△CAB≌△DAB,根据全等三角形对应边相等性质即可证明BC=BD.
解答:解:∵AB是∠CAD的角平分线
∴∠CAB=∠DAB;
∴在△CAB和△DAB中,
,
∴△CAB≌△DAB(SAS),
∴BC=BD.
∴∠CAB=∠DAB;
∴在△CAB和△DAB中,
|
∴△CAB≌△DAB(SAS),
∴BC=BD.
点评:本题考查了全等三角形的判定中SAS方法的运用,考查了全等三角形对应边相等的性质.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
在△ABC中,O为内心,∠A=70°,则∠BOC=( )
| A、140° | B、135° |
| C、130° | D、125° |
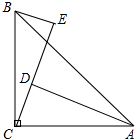 如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,BE=0.8cm,则DE的长为( )cm.
如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,BE=0.8cm,则DE的长为( )cm.| A、0.7 | B、1.7 |
| C、3.3 | D、2.3 |
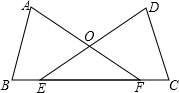 如图,已知AF=DE,AB=DC,BE=CF.求证:(1)△ABF≌△DCE;(2)△EOF是等腰三角形.
如图,已知AF=DE,AB=DC,BE=CF.求证:(1)△ABF≌△DCE;(2)△EOF是等腰三角形.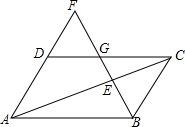 如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE.
如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE. AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=130°,∠C=30°,则∠DAE的度数是
AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=130°,∠C=30°,则∠DAE的度数是